Ressources en ligne

L’extension centrale pour l’analyse de survie est survival.

Un très bon tutoriel (en anglais et en 3 étapes), introduisant les concepts de l’analyse de survie, des courbes de Kaplan-Meier et des modèles de Cox et leur mise en oeuvre pratique sous R est disponible en ligne :

Pour un autre exemple (toujours en anglais) d’analyse de survie avec survival, on pourra se référer à https://rpubs.com/vinubalan/hrsurvival.

Pour représenter vos résultats avec ggplot2, on pourra avoir recours à l’extension survminer présentée en détails sur son site officiel (en anglais) : http://www.sthda.com/english/rpkgs/survminer/. On pourra également avoir recours à la fonction ggsurv de l’extension GGally présentée à l’adresse http://ggobi.github.io/ggally/#ggallyggsurv.

A noter, il est possible d’utiliser la fonction step sur un modèle de Cox, pour une sélection pas à pas d’un meilleur modèle basé sur une minimisation de l’AIC (voir le chapitre sur la régression logistique).

L’excellente extension broom peut également être utilisée sur des modèles de survie (Kaplan-Meier ou Cox) pour en convertir les résultats sous la forme d’un tableau de données.

Pour approfondir les possibilités offertes par l’extension survival, on pourra également consulter les différentes vignettes fournies avec l’extension (voir https://cran.r-project.org/package=survival).

Un exemple concret : mortalité infanto-juvénile

Dans cet exemple, nous allons utiliser le jeu de données fecondite fourni par l’extension questionr. Ce jeu de données comporte trois tableaux de données : menages, femmes et enfants.

Nous souhaitons étudier ici la survie des enfants entre la naissance et l’âge de 5 ans. Dans un premier temps, nous comparerons la survie des jeunes filles et des jeunes garçons. Dans un second temps, nous procéderons à une analyse multivariée en prenant en compte les variables suivantes :

  • sexe de l’enfant
  • milieu de résidence
  • niveau de vie du ménage
  • structure du ménage
  • niveau d’éducation de la mère
  • âge de la mère à la naissance de l’enfant
  • enfin, une variable un peu plus compliquée, à savoir si le rang de naissance de l’enfant (second, troisième, quatrième, etc.) est supérieur au nombre idéal d’enfants selon la mère.

Nous allons préparer les données selon deux approches : soit en utilisant l’extension data.table (voir le chapitre dédié à data.table), soit en utilisant l’extension dplyr (voir le chapitre sur dplyr).

Chargeons les données en mémoire et listons les variables disponibles.

Préparation des données avec data.table

Tout d’abord, regardons sous quel format elles sont stockées.

[1] "tbl_df"     "tbl"        "data.frame"
[1814 obs. x 5 variables] tbl_df tbl data.frame

$id_menage: Identifiant du ménage
numeric: 1 2 3 4 5 6 7 8 9 10 ...
min: 1 - max: 1814 - NAs: 0 (0%) - 1814 unique values

$taille: Taille du ménage (nombre de membres)
numeric: 7 3 6 5 7 6 15 6 5 19 ...
min: 1 - max: 31 - NAs: 0 (0%) - 30 unique values

$sexe_chef: Sexe du chef de ménage
labelled double: 2 1 1 1 1 2 2 2 1 1 ...
min: 1 - max: 2 - NAs: 0 (0%) - 2 unique values
2 value labels: [1] homme [2] femme

$structure: Structure démographique du ménage
labelled double: 4 2 5 4 4 4 5 2 5 5 ...
min: 1 - max: 5 - NAs: 0 (0%) - 5 unique values
6 value labels: [0] pas d'adulte [1] un adulte [2] deux adultes de sexe opposé [3] deux adultes de même sexe [4] trois adultes ou plus avec lien de parenté [5] adultes sans lien de parenté

$richesse: Niveau de vie (quintiles)
labelled double: 1 2 2 1 1 3 2 5 4 3 ...
min: 1 - max: 5 - NAs: 0 (0%) - 5 unique values
5 value labels: [1] très pauvre [2] pauvre [3] moyen [4] riche [5] très riche

Les tableaux de données sont au format tibble (c’est-à-dire sont de la classe tbl_df) et les variables catégorielles sont du type haven_labelled (voir le chapitre sur les vecteurs labellisés). Ce format correspond au format de données si on les avait importées depuis SPSS avec l’extension haven (voir le chapitre sur l’import de données).

En premier lieu, il nous faut convertir les tableaux de données au format data.table, ce qui peut se faire avec la fonction setDT1. Par ailleurs, nous allons également charger en mémoire l’extension labelled pour la gestion des vecteurs labellisés.

En premier lieu, il nous faut calculer la durée d’observation des enfants, à savoir le temps passé entre la date de naissance (variable du fichier enfants) et la date de passation de l’entretien (fournie par le tableau de données femmes). Pour récupérer des variables du fichier femmes dans le fichier enfants, nous allons procéder à une fusion de table (voir le chapitre dédié). Pour le calcul de la durée d’observation, nous allons utiliser le package lubridate (voir le chapitre calculer un âge et celui sur la gestion des dates). Nous effectuerons l’analyse en mois (puisque l’âge au décès est connu en mois). Dès lors, la durée d’observation sera calculée en mois.

ATTENTION : il y 11 enfants soi-disant nés après la date d’enquête ! Quelle que soit l’enquête, il est rare de ne pas observer d’incohérences. Dans le cas présent, il est fort possible que la date d’entretien puisse parfois être erronnée (par exemple si l’enquêteur a inscrit une date sur le questionnaire papier le jour du recensement du ménage mais n’ai pu effectué le questionnaire individuel que plus tard). Nous décidons ici de procéder à une correction en ajoutant un mois aux dates d’entretien problématiques. D’autres approches auraient pu être envisagées, comme par exemple exclure ces observations problématiques. Cependant, cela aurait impacté le calcul du range de naissance pour les autres enfants issus de la même mère. Quoiqu’il en soit, il n’y a pas de réponse unique. À vous de vous adapter au contexte particulier de votre analyse.

Regardons maintenant comment les âges au décès ont été collectés.

Les âges au décès sont ici exprimés en mois révolus. Les décès à un mois révolu correspondent à des décès entre 1 et 2 mois exacts. Par ailleurs, les durées d’observation que nous avons calculées avec time_length sont des durées exactes, c’est-à-dire avec la partie décimale. Pour une analyse de survie, on ne peut mélanger des durées exactes et des durées révolues. Trois approches peuvent être envisagées :

  1. faire l’analyse en mois révolus, auquel cas on ne gardera que la partie entière des durées d’observations avec la fonction trunc ;
  2. considérer qu’un âge au décès de 3 mois révolus correspond en moyenne à 3,5 mois exacts et donc ajouter 0,5 à tous les âges révolus ;
  3. imputer un âge au décès exact en distribuant aléatoirement les décès à 3 mois révolus entre 3 et 4 mois exacts, autrement dit en ajoutant aléatoirement une partie décimale aux âges révolus.

Nous allons ici adopter la troisième approche en considérant que les décès se répartissent de manière uniforme au sein d’un même mois. Nous aurons donc recours à la fonction runif qui permets de générer des valeurs aléatoires entre 0 et 1 selon une distribustion uniforme.

Pour définir notre objet de survie, il nous faudra deux variables. Une première, temporelle, indiquant la durée à laquelle survient l’évènement étudié (ici le décès) pour ceux ayant vécu l’évènement et la durée d’observation pour ceux n’ayant pas vécu l’évènement (censure à droite). Par ailleurs, une seconde variable indiquant si les individus ont vécu l’évènement (0 pour non, 1 pour oui). Or, ici, la variable survie est codée 0 pour les décès et 1 pour ceux ayant survécu. Pour plus de détails, voir l’aide de la fonction Surv.

Occupons-nous maintenant des variables explicatives que nous allons inclure dans l’analyse. Tout d’abord, ajoutons à la table enfants les variables nécessaires des tables femmes et menages. Notons qu’il nous faudra importer id_menage de la table femmes pour pouvoir fusionner ensuite la table enfants avec la table menages. Par ailleurs, pour éviter une confusion sur la variable date_naissance, nous renommons à la volée cette variable de la table femmes en date_naissance_mere.

Les variables catégorielles sont pour l’heure sous formes de vecteurs labellisés. Or, dans un modèle, il est impératif de les convertir en facteurs pour qu’elles soient bien traitées comme des variables catégorielles (autrement elles seraient traitées comme des variables continues). On aura donc recours à la fonction to_factor de l’extension labelled.

Regardons plus attentivement, la variable structure.

Tout d’abord, la modalité pas d’adulte n’est pas représentée dans l’échantillon. On aura donc recours à l’argument drop_unused_labels pour ne pas conserver cette modalité. Par ailleurs, nous considérons que la situation familiale à partir de laquelle nous voudrons comparer les autres dans notre modèle, donc celle qui doit être considérée comme la modalité de référence, est celle du ménage nucléaire. Cette modalité (deux adultes de sexe opposé) n’étant pas la première, nous aurons recours à la fonction relevel.

Regardons la variable educ.

La modalité supérieur est peu représentée dans notre échantillon. Nous allons la fusionner avec la modalité secondaire (voir la section Regrouper les modalités d’une variable du chapitre Recodage).

Calculons maintenant l’âge de la mère à la naissance de l’enfant (voir le chapitre Calculer un âge) et découpons le en groupes d’âges (voir la section Découper une variable numérique en classes du chapitre Recodage).

Reste à calculer si le rang de naissance de l’enfant est supérieur au nombre idéal d’enfants tel que défini par la mère. On aura recours à la fonction rank appliquée par groupe (ici calculé séparément pour chaque mère). L’argument ties.method permet d’indiquer comment gérer les égalités (ici les naissances multiples, e.g. les jumeaux). Comme nous voulons comparer le rang de l’enfant au nombre idéal d’enfants, nous allons retenir la méthode "max" pour obtenir, dans le cas présent, le nombre total d’enfants déjà nés2. Avant de calculer un rang, il est impératif de trier préalablement le tableau (voir le chapitre Tris).

Préparation des données avec dplyr

Tout d’abord, regardons sous quel format elles sont stockées.

[1] "tbl_df"     "tbl"        "data.frame"
[1814 obs. x 5 variables] tbl_df tbl data.frame

$id_menage: Identifiant du ménage
numeric: 1 2 3 4 5 6 7 8 9 10 ...
min: 1 - max: 1814 - NAs: 0 (0%) - 1814 unique values

$taille: Taille du ménage (nombre de membres)
numeric: 7 3 6 5 7 6 15 6 5 19 ...
min: 1 - max: 31 - NAs: 0 (0%) - 30 unique values

$sexe_chef: Sexe du chef de ménage
labelled double: 2 1 1 1 1 2 2 2 1 1 ...
min: 1 - max: 2 - NAs: 0 (0%) - 2 unique values
2 value labels: [1] homme [2] femme

$structure: Structure démographique du ménage
labelled double: 4 2 5 4 4 4 5 2 5 5 ...
min: 1 - max: 5 - NAs: 0 (0%) - 5 unique values
6 value labels: [0] pas d'adulte [1] un adulte [2] deux adultes de sexe opposé [3] deux adultes de même sexe [4] trois adultes ou plus avec lien de parenté [5] adultes sans lien de parenté

$richesse: Niveau de vie (quintiles)
labelled double: 1 2 2 1 1 3 2 5 4 3 ...
min: 1 - max: 5 - NAs: 0 (0%) - 5 unique values
5 value labels: [1] très pauvre [2] pauvre [3] moyen [4] riche [5] très riche

Les tableaux de données sont déjà au format tibble (c’est-à-dire sont de la classe tbl_df)3 et les variables catégorielles sont du type labelled (voir le chapitre sur les vecteurs labellisés). Ce format correspond au format de données si on les avait importées depuis SPSS avec l’extension haven (voir le chapitre sur l’import de données).

Nous allons charger en mémoire l’extension labelled pour la gestion des vecteurs labellisés en plus de dplyr.

En premier lieu, il nous faut calculer la durée d’observation des enfants, à savoir le temps passé entre la date de naissance (variable du fichier enfants) et la date de passation de l’entretien (fournie par le tableau de données femmes). Pour récupérer des variables du fichier femmes dans le fichier enfants, nous allons procéder à une fusion de table (voir le chapitre dédié). Pour le calcul de la durée d’observation, nous allons utiliser le package lubridate (voir le chapitre calculer un âge et celui sur la gestion des dates). Nous effectuerons l’analyse en mois (puisque l’âge au décès est connu en mois). Dès lors, la durée d’observation sera calculée en mois.

Warning: Column `id_femme` has different attributes on LHS
and RHS of join

ATTENTION : il y 11 enfants soi-disant nés après la date d’enquête ! Quelle que soit l’enquête, il est rare de ne pas observer d’incohérences. Dans le cas présent, il est fort possible que la date d’entretien puisse parfois être erronnée (par exemple si l’enquêteur a inscrit une date sur le questionnaire papier le jour du recensement du ménage mais n’ai pu effectué le questionnaire individuel que plus tard). Nous décidons ici de procéder à une correction en ajoutant un mois aux dates d’entretien problématiques. D’autres approches auraient pu être envisagées, comme par exemple exclure ces observations problématiques. Cependant, cela aurait impacté le calcul du range de naissance pour les autres enfants issus de la même mère. Quoiqu’il en soit, il n’y a pas de réponse unique. À vous de vous adapter au contexte particulier de votre analyse.

Regardons maintenant comment les âges au décès ont été collectés.

Les âges au décès sont ici exprimés en mois révolus. Les décès à un mois révolu correspondent à des décès entre 1 et 2 mois exacts. Par ailleurs, les durées d’observation que nous avons calculées avec time_length sont des durées exactes, c’est-à-dire avec la partie décimale. Pour une analyse de survie, on ne peut mélanger des durées exactes et des durées révolues. Trois approches peuvent être envisagées :

  1. faire l’analyse en mois révolus, auquel cas on ne gardera que la partie entière des durées d’observations avec la fonction trunc ;
  2. considérer qu’un âge au décès de 3 mois révolus correspond en moyenne à 3,5 mois exacts et donc ajouter 0,5 à tous les âges révolus ;
  3. imputer un âge au décès exact en distribuant aléatoirement les décès à 3 mois révolus entre 3 et 4 mois exacts, autrement dit en ajoutant aléatoirement une partie décimale aux âges révolus.

Nous allons ici adopter la troisième approche en considérant que les décès se répartissent de manière uniforme au sein d’un même mois. Nous aurons donc recours à la fonction runif qui permets de générer des valeurs aléatoires entre 0 et 1 selon une distribustion uniforme.

Pour définir notre objet de survie, il nous faudra deux variables. Une première, temporelle, indiquant la durée à laquelle survient l’évènement étudié (ici le décès) pour ceux ayant vécu l’évènement et la durée d’observation pour ceux n’ayant pas vécu l’évènement (censure à droite). Par ailleurs, une seconde variable indiquant si les individus ont vécu l’évènement (0 pour non, 1 pour oui). Or, ici, la variable survie est codée 0 pour les décès et 1 pour ceux ayant survécu. Pour plus de détails, voir l’aide de la fonction Surv.

Occupons-nous maintenant des variables explicatives que nous allons inclure dans l’analyse. Tout d’abord, ajoutons à la table enfants les variables nécessaires des tables femmes et menages. Notons qu’il nous faudra importer id_menage de la table femmes pour pouvoir fusionner ensuite la table enfants avec la table menages. Par ailleurs, pour éviter une confusion sur la variable date_naissance, nous renommons à la volée cette variable de la table femmes en date_naissance_mere.

Warning: Column `id_femme` has different attributes on LHS
and RHS of join

Les variables catégorielles sont pour l’heure sous formes de vecteurs labellisés. Or, dans un modèle, il est impératif de les convertir en facteurs pour qu’elles soient bien traitées comme des variables catégorielles (autrement elles seraient traitées comme des variables continues). On aura donc recours à la fonction to_factor de l’extension labelled.

Regardons plus attentivement, la variable structure.

Tout d’abord, la modalité pas d’adulte n’est pas représentée dans l’échantillon. On aura donc recours à l’argument drop_unused_labels pour ne pas conserver cette modalité. Par ailleurs, nous considérons que la situation familiale à partir de laquelle nous voudrons comparer les autres dans notre modèle, donc celle qui doit être considérée comme la modalité de référence, est celle du ménage nucléaire. Cette modalité (deux adultes de sexe opposé) n’étant pas la première, nous aurons recours à la fonction relevel{data-pkg = “stats”}.

Regardons la variable educ.

La modalité supérieur est peu représentée dans notre échantillon. Nous allons la fusionner avec la modalité secondaire (voir la section Regrouper les modalités d’une variable du chapitre Recodage).

Calculons maintenant l’âge de la mère à la naissance de l’enfant (voir le chapitre Caluler un âge) et découpons le en groupes d’âges (voir la section Découper une variable numérique en classes du chapitre Recodage).

Reste à calculer si le rang de naissance de l’enfant est supérieur au nombre idéal d’enfants tel que défini par la mère. On aura recours à la fonction rank appliquée par groupe (ici calculé séparément pour chaque mère). L’argument ties.method permet d’indiquer comment gérer les égalités (ici les naissances multiples, e.g. les jumeaux). Comme nous voulons comparer le rang de l’enfant au nombre idéal d’enfants, nous allons retenir la méthode "max" pour obtenir, dans le cas présent, le nombre total d’enfants déjà nés4. Avant de calculer un rang, il est impératif de trier préalablement le tableau (voir le chapitre Tris).

Kaplan-Meier

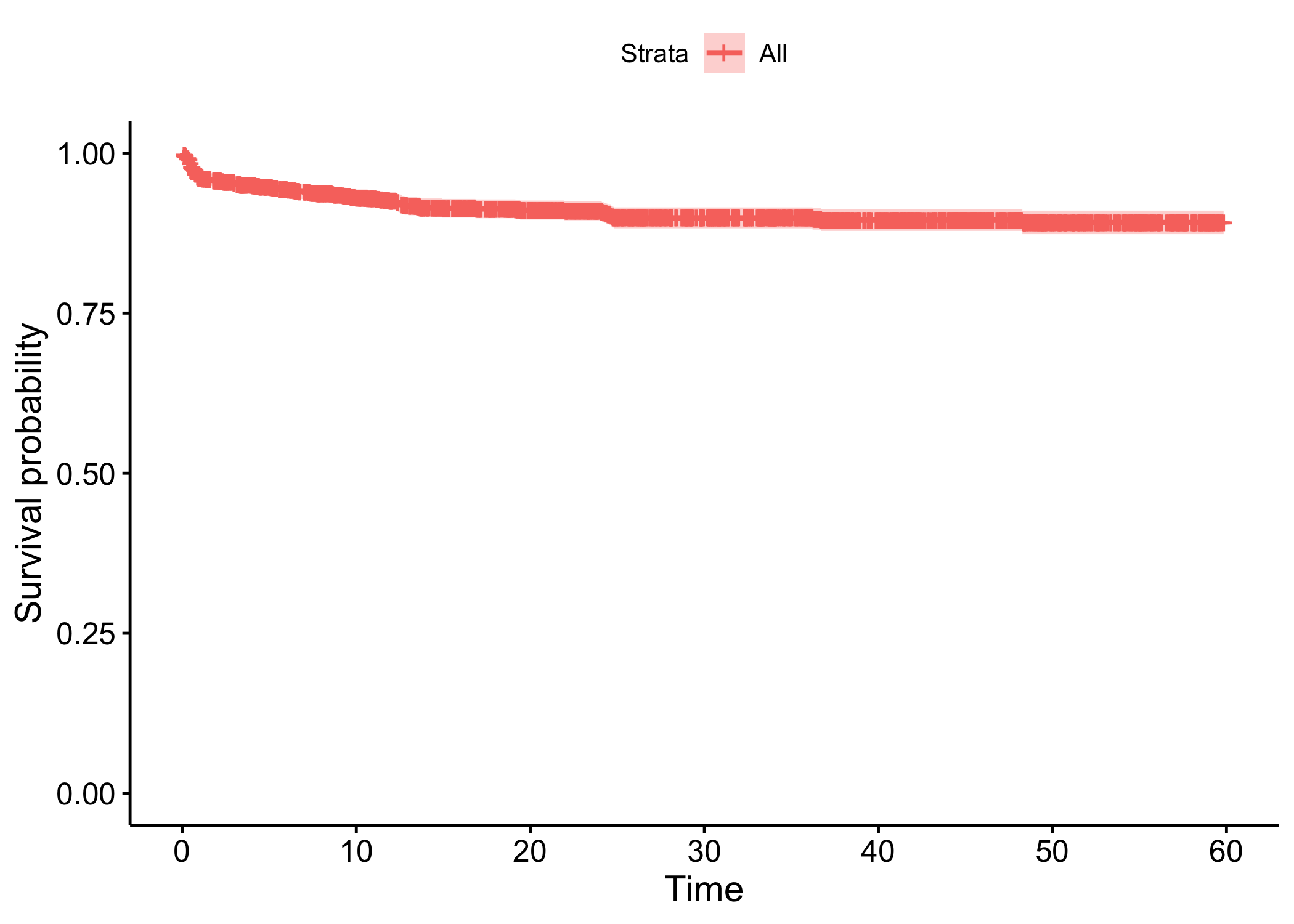
La courbe de survie de Kaplan-Meier s’obtient avec la fonction survfit de l’extension survival.

Call: survfit(formula = Surv(time, deces) ~ 1, data = enfants)

      n  events  median 0.95LCL 0.95UCL 
   1584     142      NA      NA      NA

Pour la représenter, on pourra avoir recours à la fonction ggsurvplot de l’extension survminer.

Courbe de survie de Kaplan-Meier

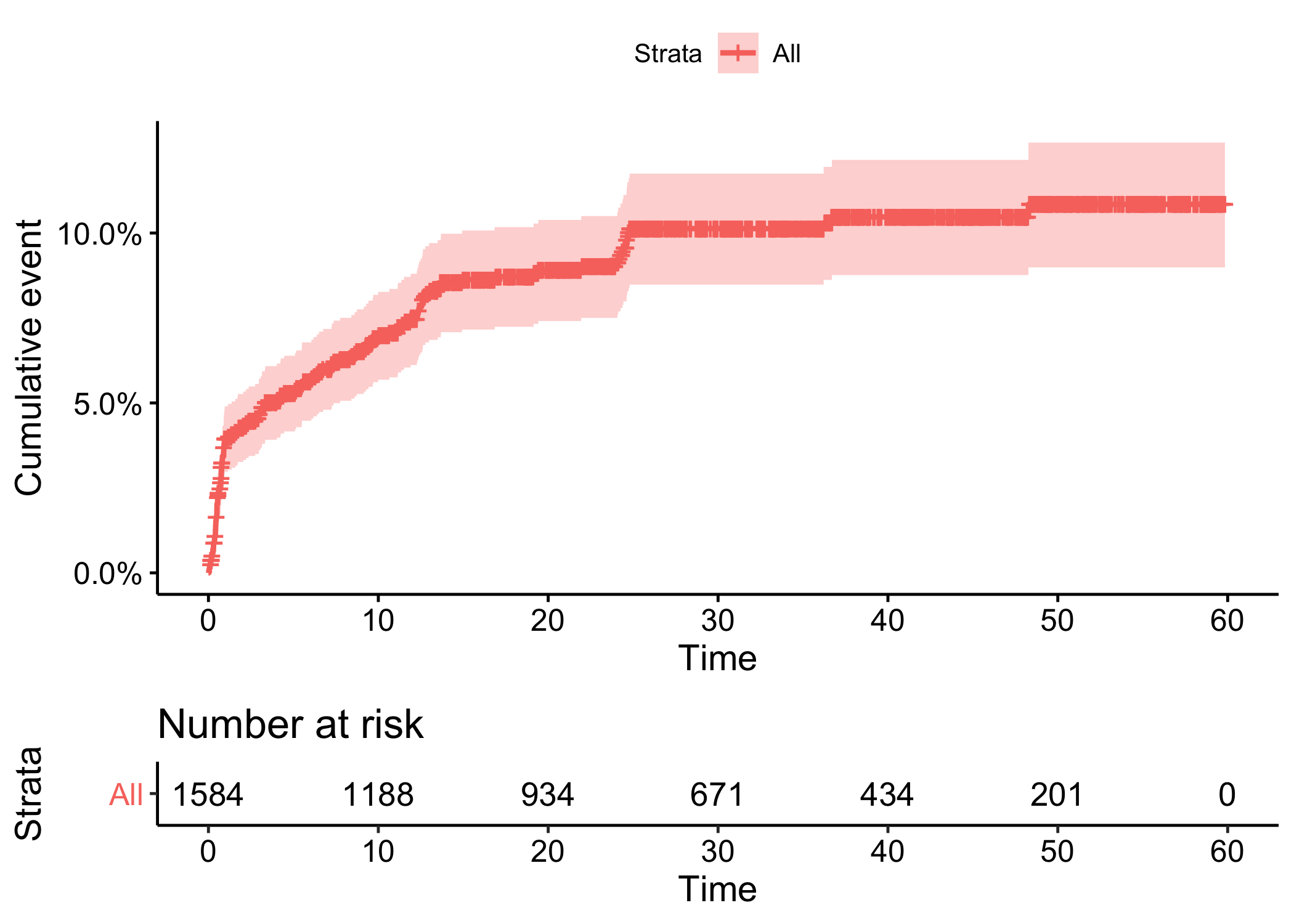
On peut facilement représenter à la place la courbe cumulée des évènements (l’inverse de la courbe de survie) et la table des effectifs en fonction du temps.

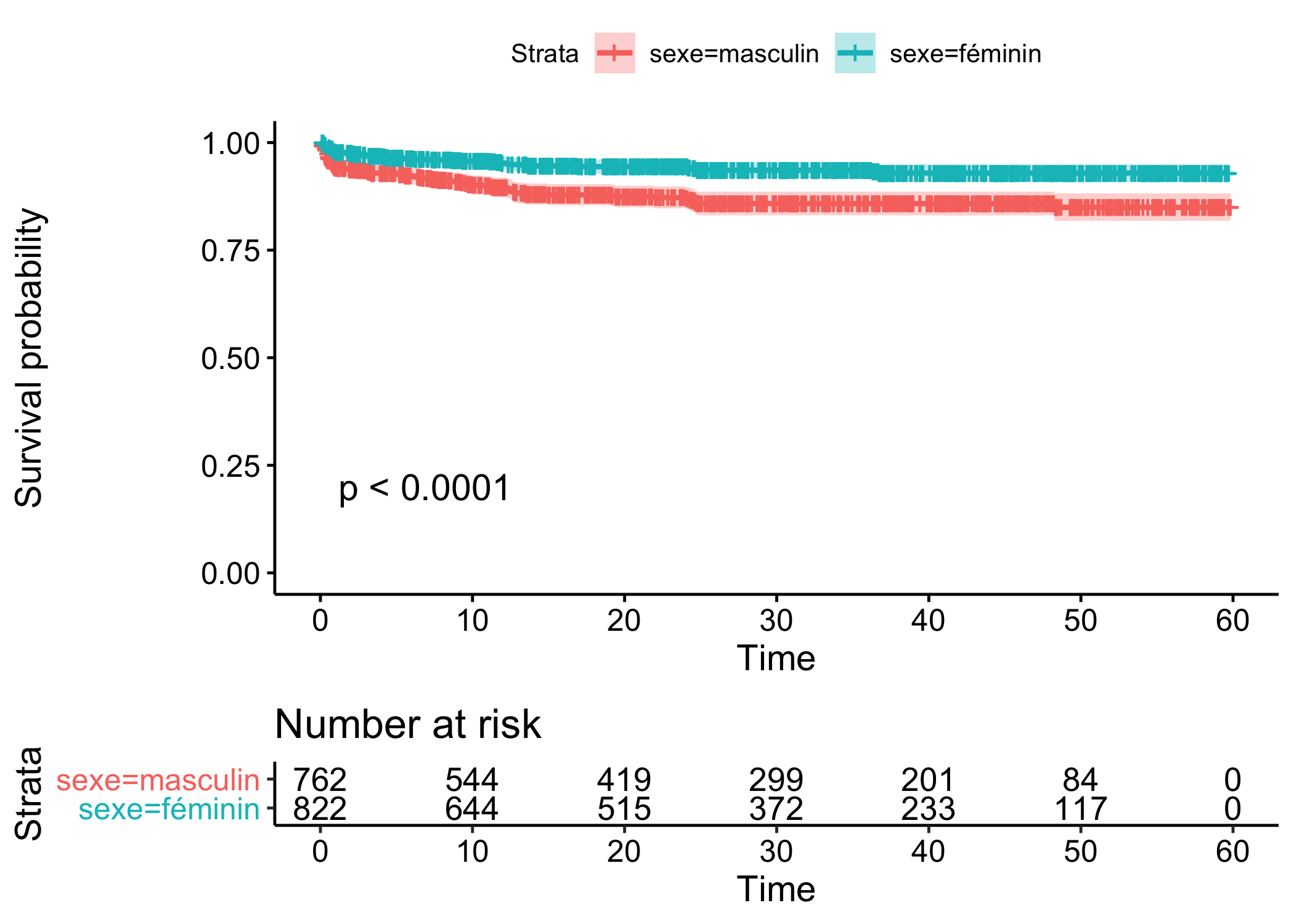
Courbe cumulée des évènements et table des effectifs

Pour comparer deux groupes (ici les filles et les garçons), il suffit d’indiquer la variable de comparaison à survfit.

Call: survfit(formula = Surv(time, deces) ~ sexe, data = enfants)

                n events median 0.95LCL 0.95UCL
sexe=masculin 762     94     NA      NA      NA
sexe=féminin  822     48     NA      NA      NA

La fonction survdiff permets de calculer le test du logrank afin de comparer des courbes de survie. La mortalité infanto-juvénile diffère-t-elle significativement selon le sexe de l’enfant ?

Call:
survdiff(formula = Surv(time, deces) ~ sexe, data = enfants)

                N Observed Expected (O-E)^2/E (O-E)^2/V
sexe=masculin 762       94     66.2      11.6      21.8
sexe=féminin  822       48     75.8      10.2      21.8

 Chisq= 21.8  on 1 degrees of freedom, p= 3e-06

Une fois encore, on aura recours à ggsurvplot pour représenter les courbes de survie.

Courbes de Kaplan-Meier selon le sexe

Modèle de Cox

Un modèle de Cox se calcule aisément avec coxph{survival}.

Call:
coxph(formula = Surv(time, deces) ~ sexe + milieu + richesse + 
    structure + educ2 + gpage_mere_naissance + rang_apres_ideal, 
    data = enfants)

                                                         coef
sexeféminin                                         -0.809568
milieu                                               0.656241
richessepauvre                                      -0.082223
richessemoyen                                        0.318645
richesseriche                                        0.353483
richessetrès riche                                   0.464590
structureun adulte                                  -0.150231
structuredeux adultes de même sexe                   0.604592
structuretrois adultes ou plus avec lien de parenté  0.049430
structureadultes sans lien de parenté               -0.131369
educ2primaire                                       -0.030251
educ2secondaire ou plus                             -0.203903
gpage_mere_naissance19 ou moins                     -0.310248
gpage_mere_naissance30 et plus                      -0.002586
rang_apres_idealoui                                  1.355106
                                                    exp(coef)
sexeféminin                                          0.445050
milieu                                               1.927533
richessepauvre                                       0.921066
richessemoyen                                        1.375263
richesseriche                                        1.424019
richessetrès riche                                   1.591361
structureun adulte                                   0.860509
structuredeux adultes de même sexe                   1.830506
structuretrois adultes ou plus avec lien de parenté  1.050672
structureadultes sans lien de parenté                0.876895
educ2primaire                                        0.970202
educ2secondaire ou plus                              0.815541
gpage_mere_naissance19 ou moins                      0.733265
gpage_mere_naissance30 et plus                       0.997417
rang_apres_idealoui                                  3.877173
                                                     se(coef)
sexeféminin                                          0.177806
milieu                                               0.269928
richessepauvre                                       0.250417
richessemoyen                                        0.247868
richesseriche                                        0.298425
richessetrès riche                                   0.428583
structureun adulte                                   0.600329
structuredeux adultes de même sexe                   0.376445
structuretrois adultes ou plus avec lien de parenté  0.196666
structureadultes sans lien de parenté                0.305478
educ2primaire                                        0.205751
educ2secondaire ou plus                              0.366889
gpage_mere_naissance19 ou moins                      0.268062
gpage_mere_naissance30 et plus                       0.191557
rang_apres_idealoui                                  0.602401
                                                         z
sexeféminin                                         -4.553
milieu                                               2.431
richessepauvre                                      -0.328
richessemoyen                                        1.286
richesseriche                                        1.184
richessetrès riche                                   1.084
structureun adulte                                  -0.250
structuredeux adultes de même sexe                   1.606
structuretrois adultes ou plus avec lien de parenté  0.251
structureadultes sans lien de parenté               -0.430
educ2primaire                                       -0.147
educ2secondaire ou plus                             -0.556
gpage_mere_naissance19 ou moins                     -1.157
gpage_mere_naissance30 et plus                      -0.014
rang_apres_idealoui                                  2.250
                                                           p
sexeféminin                                         5.29e-06
milieu                                                0.0151
richessepauvre                                        0.7427
richessemoyen                                         0.1986
richesseriche                                         0.2362
richessetrès riche                                    0.2784
structureun adulte                                    0.8024
structuredeux adultes de même sexe                    0.1083
structuretrois adultes ou plus avec lien de parenté   0.8016
structureadultes sans lien de parenté                 0.6672
educ2primaire                                         0.8831
educ2secondaire ou plus                               0.5784
gpage_mere_naissance19 ou moins                       0.2471
gpage_mere_naissance30 et plus                        0.9892
rang_apres_idealoui                                   0.0245

Likelihood ratio test=38.16  on 15 df, p=0.0008546
n= 1584, number of events= 142

De nombreuses variables ne sont pas significatives. Voyons si nous pouvons, avec la fonction step, améliorer notre modèle par minimisation de l’AIC ou Akaike Information Criterion (voir la section Sélection de modèles du chapitre sur la Régression logistique).

Start:  AIC=2027.07
Surv(time, deces) ~ sexe + milieu + richesse + structure + educ2 + 
    gpage_mere_naissance + rang_apres_ideal

                       Df    AIC
- structure             4 2022.0
- richesse              4 2022.7
- educ2                 2 2023.4
- gpage_mere_naissance  2 2024.6
<none>                    2027.1
- rang_apres_ideal      1 2028.6
- milieu                1 2031.3
- sexe                  1 2047.1

Step:  AIC=2022.01
Surv(time, deces) ~ sexe + milieu + richesse + educ2 + gpage_mere_naissance + 
    rang_apres_ideal

                       Df    AIC
- richesse              4 2017.0
- educ2                 2 2018.2
- gpage_mere_naissance  2 2019.5
<none>                    2022.0
- rang_apres_ideal      1 2023.4
- milieu                1 2025.6
- sexe                  1 2042.2

Step:  AIC=2017
Surv(time, deces) ~ sexe + milieu + educ2 + gpage_mere_naissance + 
    rang_apres_ideal

                       Df    AIC
- educ2                 2 2013.3
- gpage_mere_naissance  2 2014.8
<none>                    2017.0
- rang_apres_ideal      1 2018.0
- milieu                1 2018.8
- sexe                  1 2037.6

Step:  AIC=2013.28
Surv(time, deces) ~ sexe + milieu + gpage_mere_naissance + rang_apres_ideal

                       Df    AIC
- gpage_mere_naissance  2 2011.2
<none>                    2013.3
- rang_apres_ideal      1 2014.3
- milieu                1 2015.7
- sexe                  1 2033.8

Step:  AIC=2011.17
Surv(time, deces) ~ sexe + milieu + rang_apres_ideal

                   Df    AIC
<none>                2011.2
- rang_apres_ideal  1 2012.3
- milieu            1 2013.9
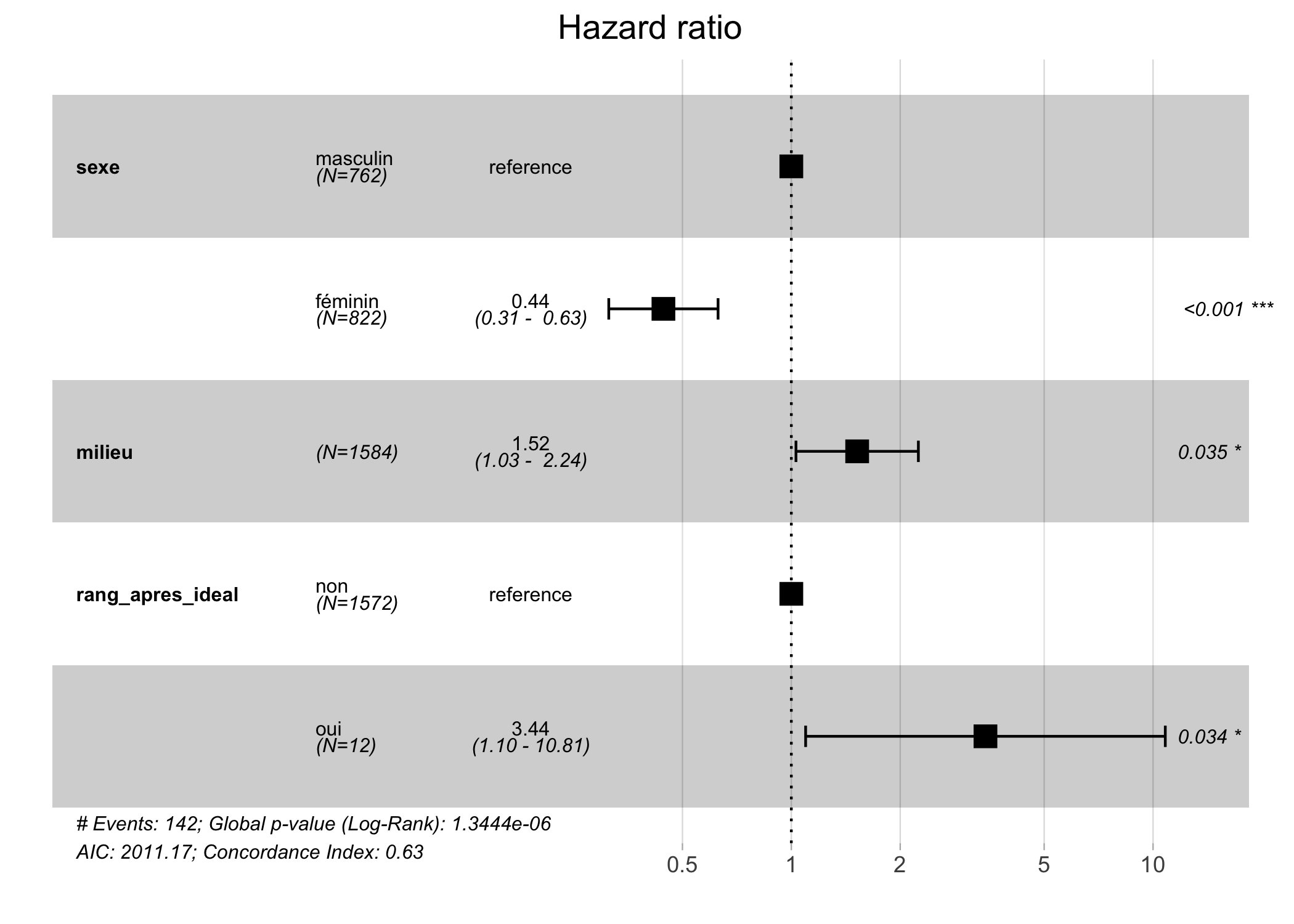
- sexe              1 2031.6

On peut obtenir facilement les coefficients du modèle avec l’excellente fonction tidy de l’extension broom. Ne pas oublier de préciser exponentiate = TRUE. En effet, dans le cas d’un modèle de Cox, l’exponentiel des coefficients corresponds au ratio des risques instantannés ou hazard ratio (HR) en anglais.

Pour représenter ces rapports de risque, on peut ici encore avoir recours à la fonction ggcoef de l’extension GGally.

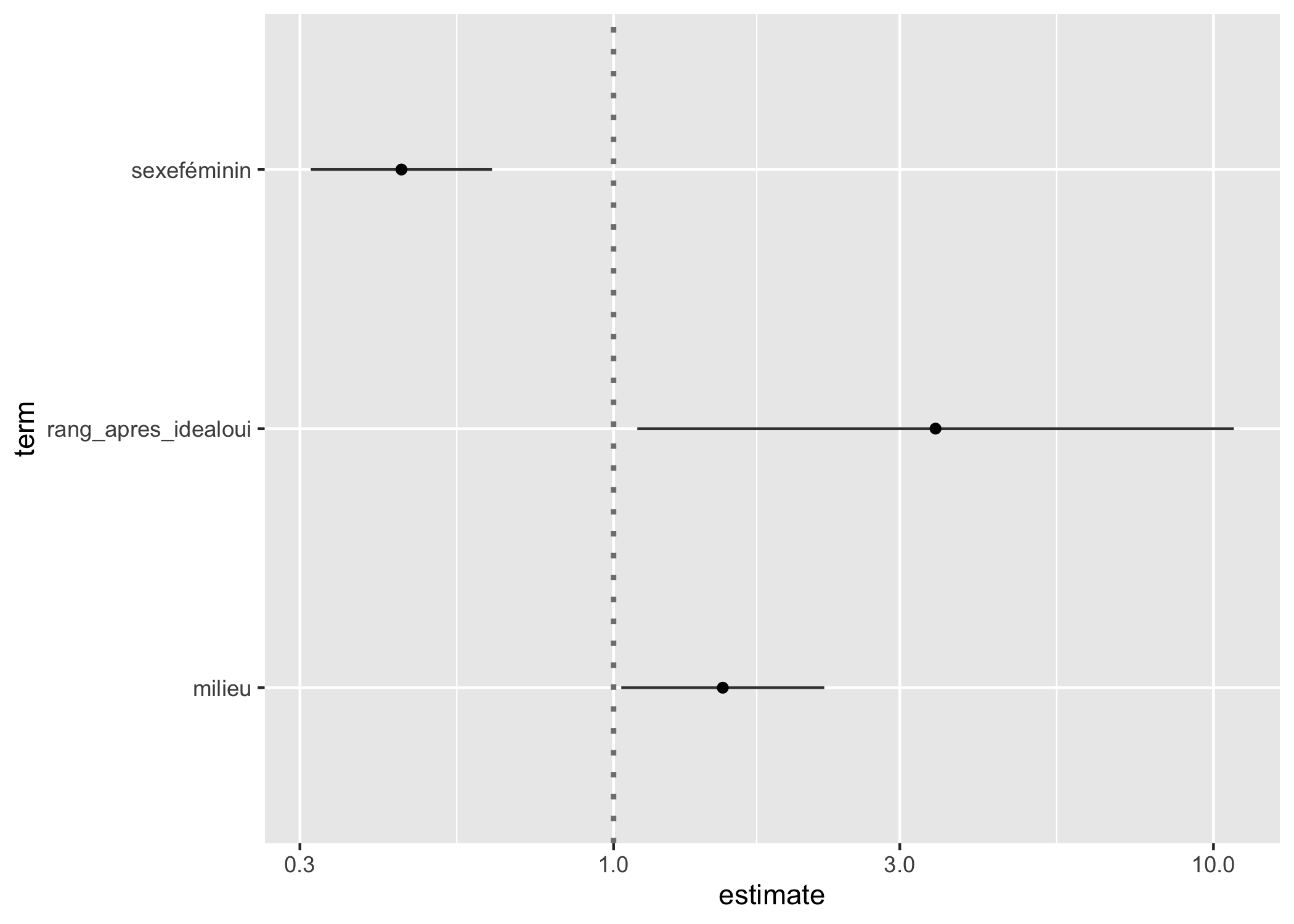
Coefficients du modèle avec ggcoef

L’extension survminer fournit également une fonction ggforest qui permet de représenter de manière plus esthétique et complète les coefficients d’un modèle de Cox.

Coefficients du modèle avec ggforest

Vérification de la validité du modèle

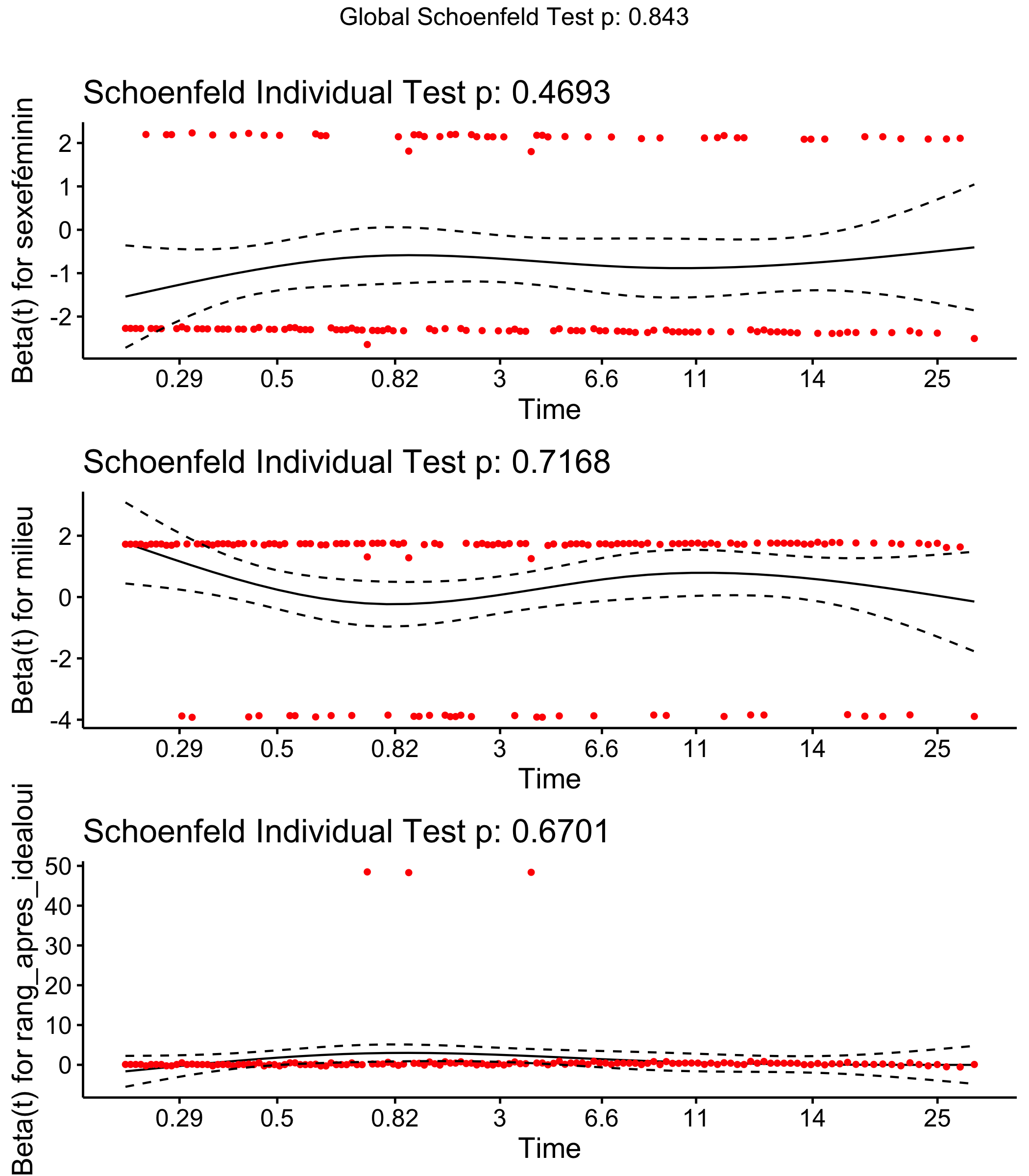
Un modèle de Cox n’est valable que sous l’hypothèse de la proportionnalité des risques relatifs. Selon cette hypothèse les résidus de Schoenfeld ne dépendent pas du temps. Cette hypothèse peut être testée avec la fonction cox.zph.

                        rho chisq     p
sexeféminin          0.0608 0.524 0.469
milieu              -0.0305 0.132 0.717
rang_apres_idealoui -0.0359 0.181 0.670
GLOBAL                   NA 0.827 0.843

Une valeur de p inférieure à 5 % indique que l’hypothèse n’est pas vérifiée. Il apparaît que p est supérieur à 5 % globalement et pour chaque variable prise individuellement. Notre modèle est donc valide.

Il est possible de représenter la distribution des résidus de Schoenfeld à l’aide de ggcoxzph de l’extension survminer, afin de voir si leur répartition change au cours du temps.

Résidus de Schoenfeld

Données pondérées

Si vous utilisez des données pondérées avec un plan d’échantillonnage complexe (voir le chapitre dédié), vous pouvez utilisez les fonctions suivantes de l’extension survey :

  • svykm pour estimer une courbe de survie de Kaplan-Meier ;
  • svycoxph pour un modèle de Cox.

Dans les deux cas, pensez à ajouter l’option se = TRUE pour que les erreurs standards soient calculées (et que les intervalles de confiance puissent être générés).

  1. Pour utiliser simultanément data.table et dplyr, nous aurions préféré la fonction tbl_dt de l’extension dtplyr.↩

  2. Ici, pour plus de simplicité, nous n’avons pas pris en compte les décès éventuels des enfants de rang inférieur avant la naissance considérée.↩

  3. Si cela n’avait pas été le cas, nous aurions eu recours à la fonction tbl_df.↩

  4. Ici, pour plus de simplicité, nous n’avons pas pris en compte les décès éventuels des enfants de rang inférieur avant la naissance considérée.↩