Statistique univariée
On entend par statistique univariée l’étude d’une seule variable, que celle-ci soit quantitative ou qualitative. La statistique univariée fait partie de la statistique descriptive.
Nous utiliserons dans ce chapitre les données de l’enquête Histoire de vie 2003 fournies avec l’extension questionr.
Variable quantitative
Principaux indicateurs
Comme la fonction str nous l’a indiqué, notre tableau d contient plusieurs variables numériques ou variables quantitatives, dont la variable heures.tv qui représente le nombre moyen passé par les enquêtés à regarder la télévision quotidiennement. On peut essayer de déterminer quelques caractéristiques de cette variable, en utilisant les fonctions mean (moyenne), sd (écart-type), min (minimum), max (maximum) et range (étendue) :
[1] NA[1] 2.247[1] 1.776[1] 0[1] 12[1] 0 12On peut lui ajouter la fonction median qui donne la valeur médiane, quantile qui calcule plus généralement tout type de quantiles, et le très utile summary qui donne toutes ces informations ou presque en une seule fois, avec en prime le nombre de valeurs manquantes (NA) :
[1] 2 0% 25% 50% 75% 100%
0 1 2 3 12 Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.00 1.00 2.00 2.25 3.00 12.00 5 La fonction summary est une fonction générique qui peut être utilisée sur tout type d’objet, y compris un tableau de données. Essayez donc summary(d).
Histogramme
Tout cela est bien pratique, mais pour pouvoir observer la distribution des valeurs d’une variable quantitative, il n’y a quand même rien de mieux qu’un bon graphique.
On peut commencer par un histogramme de la répartition des valeurs. Celui-ci peut être généré très facilement avec la fonction hist :
hist(d$heures.tv, main = "Nombre d'heures passées devant la télé par jour",
xlab = "Heures", ylab = "Effectif")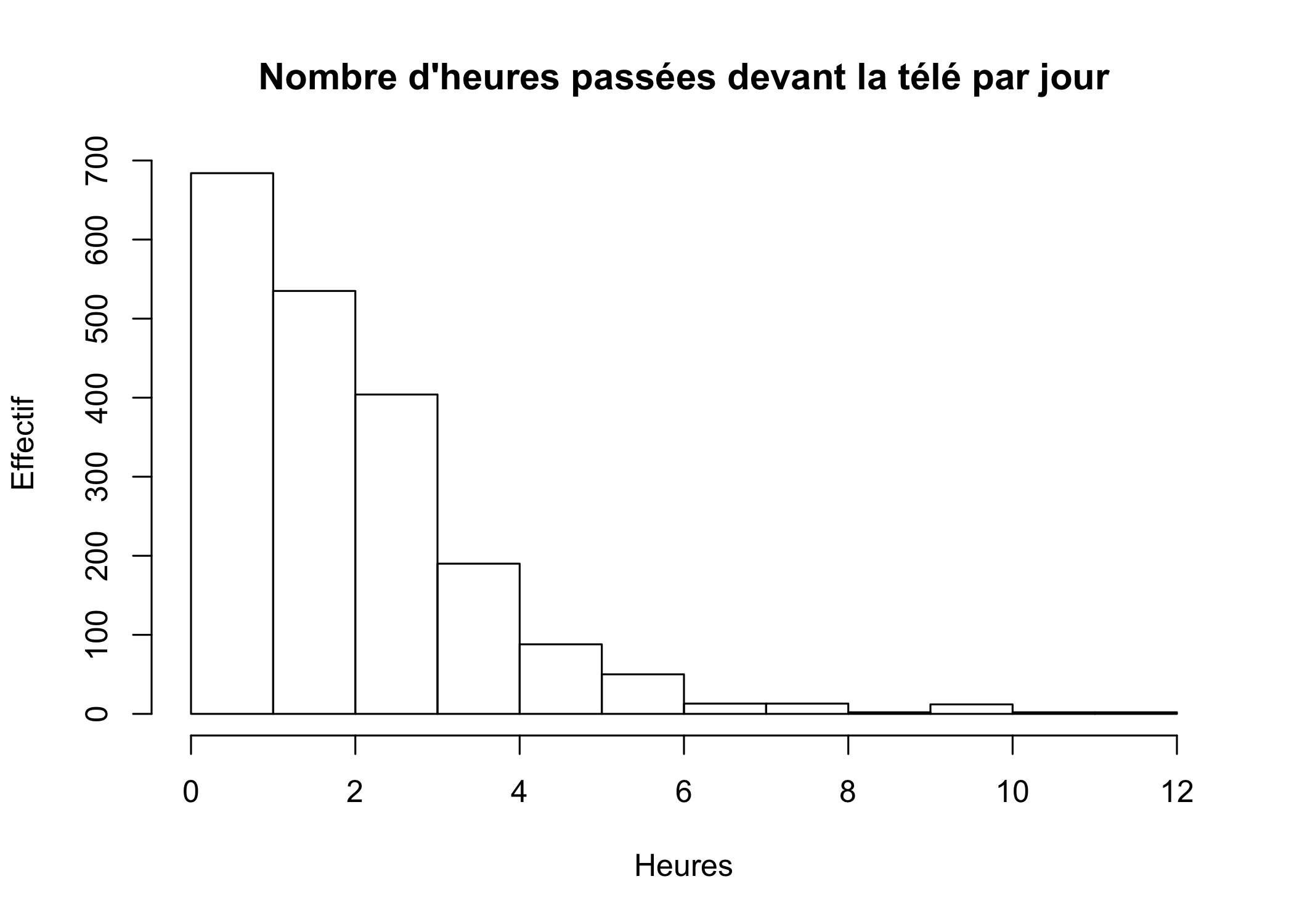
Sous RStudio, les graphiques s’affichent dans l’onglet Plots du quadrant inférieur droit. Il est possible d’afficher une version plus grande de votre graphique en cliquant sur Zoom.
Ici, les options main, xlab et ylab permettent de personnaliser le titre du graphique, ainsi que les étiquettes des axes. De nombreuses autres options existent pour personnaliser l’histogramme, parmi celles-ci on notera :
probabilitysi elle vautTRUE, l’histogramme indique la proportion des classes de valeurs au lieu des effectifs.breakspermet de contrôler les classes de valeurs. On peut lui passer un chiffre, qui indiquera alors le nombre de classes, un vecteur, qui indique alors les limites des différentes classes, ou encore une chaîne de caractère ou une fonction indiquant comment les classes doivent être calculées.colla couleur de l’histogramme1.
Voir la page d’aide de la fonction hist pour plus de détails sur les différentes options. Les deux figures ci-après sont deux autres exemples d’histogramme.
hist(d$heures.tv, main = "Heures de télé en 7 classes", breaks = 7,
xlab = "Heures", ylab = "Proportion", probability = TRUE,
col = "orange")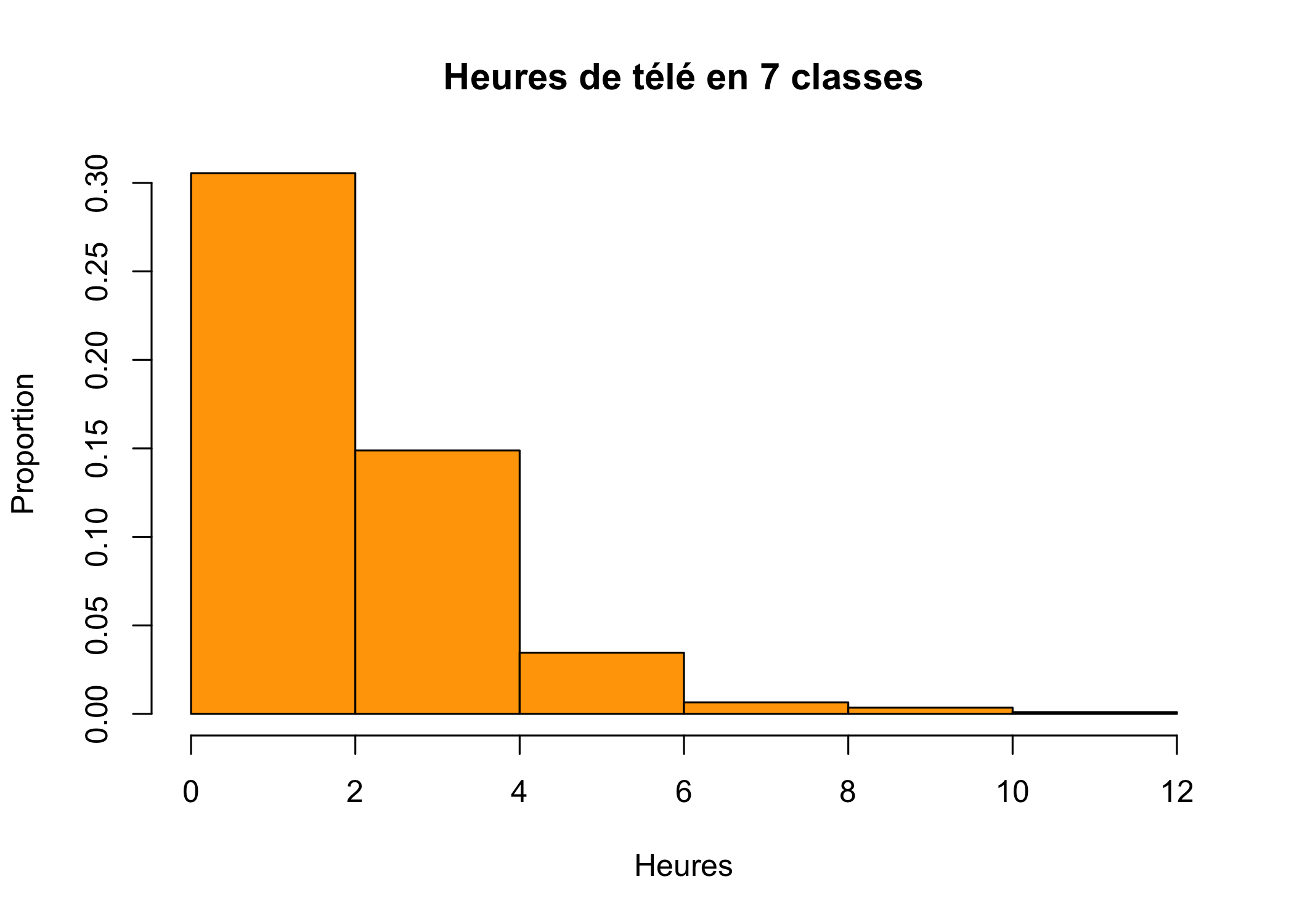
hist(d$heures.tv, main = "Heures de télé avec classes spécifiées",
breaks = c(0, 1, 4, 9, 12), xlab = "Heures", ylab = "Proportion",
col = "red")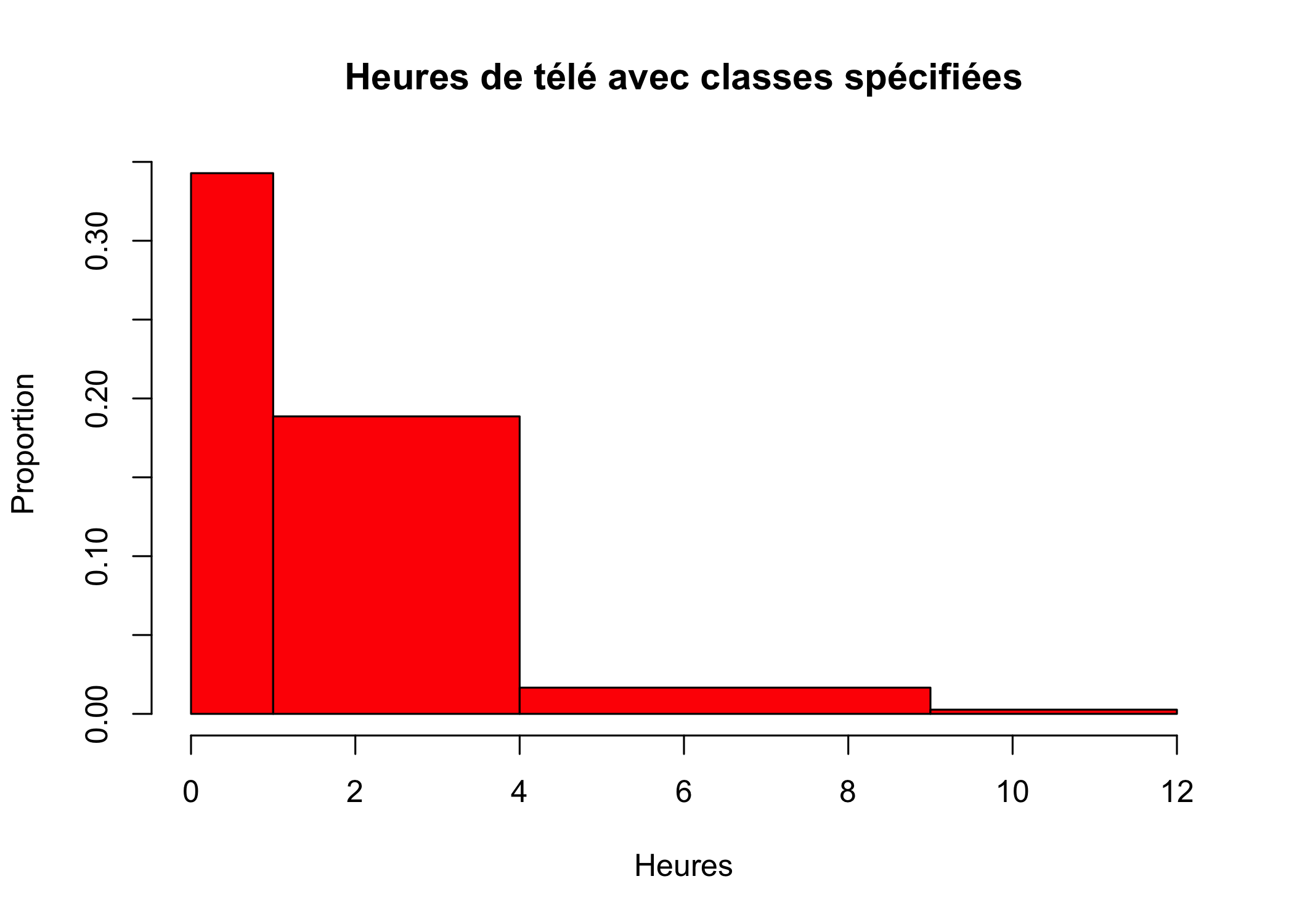
Densité et répartition cumulée
La fonction density permet d’obtenir une estimation par noyau2 de la distribution du nombre d’heures consacrées à regarder la télévision. Le paramètre na.rm = TRUE indique que l’on souhaite retirer les valeurs manquantes avant de calculer cette courbe de densité.
Le résultat de cette estimation est ensuite représenté graphiquement à l’aide de plot. L’argument main permet de spécifier le titre du graphique.
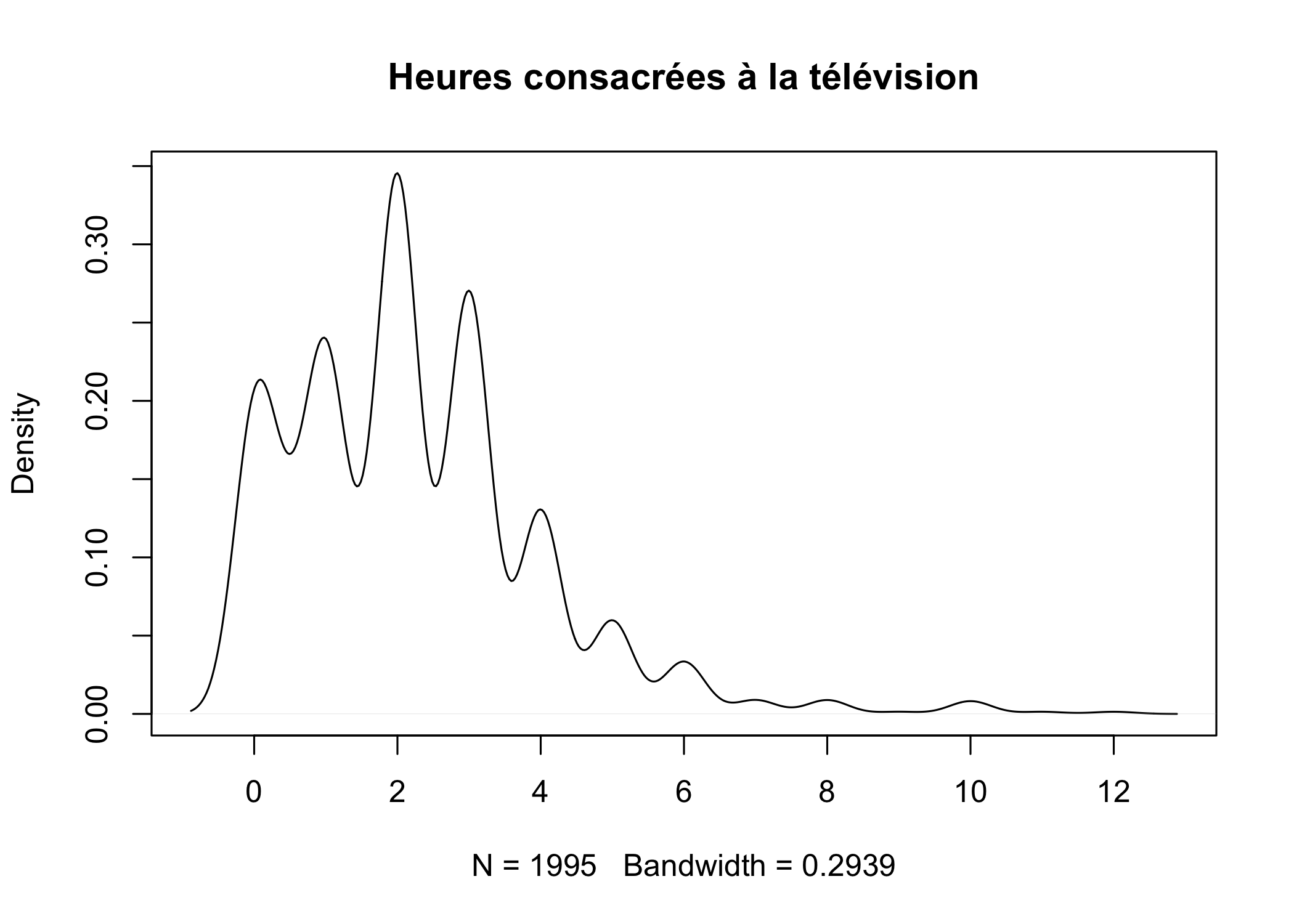
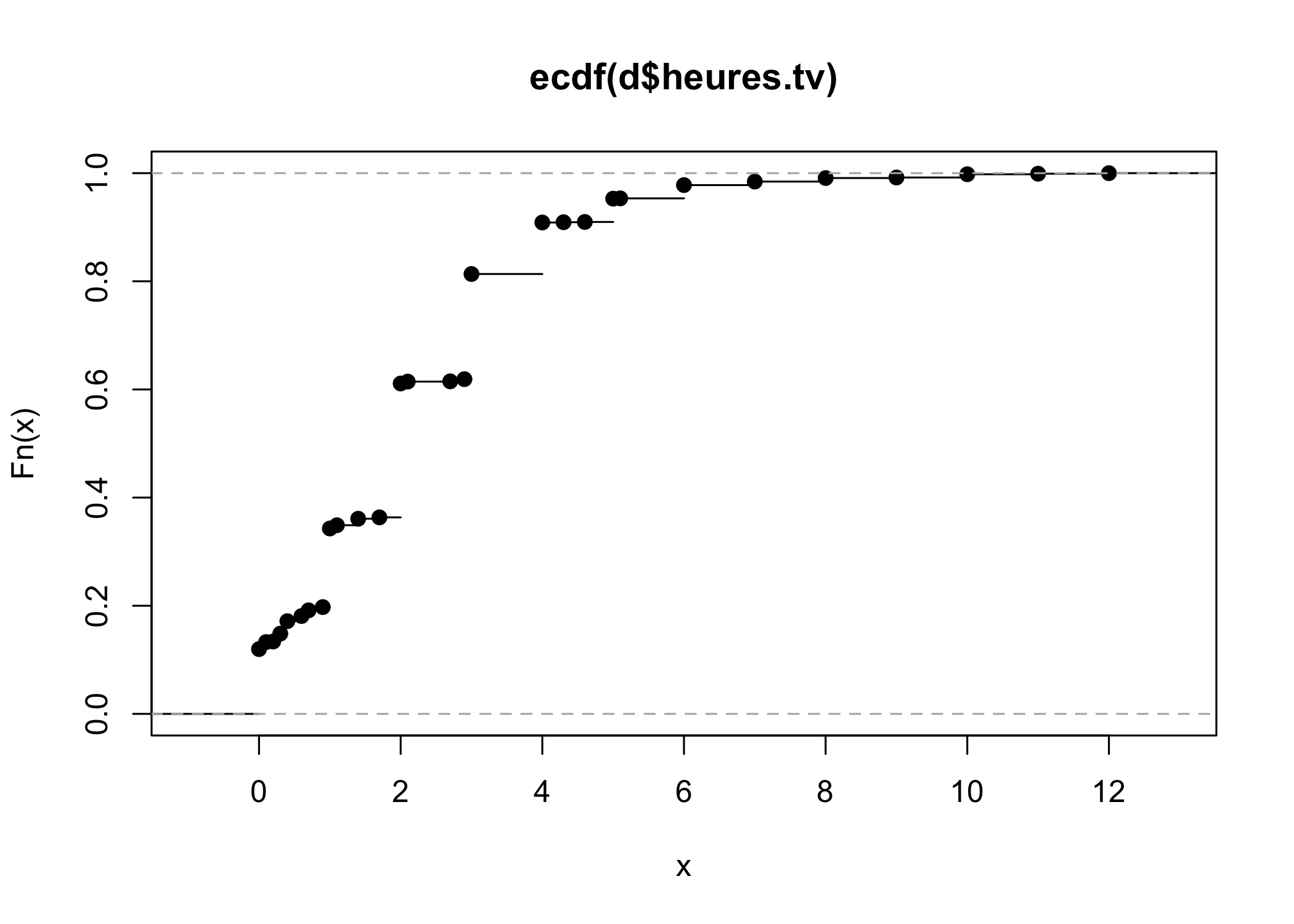
De manière similaire, on peut calculer la fonction de répartition empirique ou empirical cumulative distribution function en anglais avec la fonction ecdf. Le résultat obtenu peut, une fois encore, être représenté sur un graphique à l’aide de la fonction plot.
Boîtes à moustaches
Les boîtes à moustaches, ou boxplots en anglais, sont une autre représentation graphique de la répartition des valeurs d’une variable quantitative. Elles sont particulièrement utiles pour comparer les distributions de plusieurs variables ou d’une même variable entre différents groupes, mais peuvent aussi être utilisées pour représenter la dispersion d’une unique variable. La fonction qui produit ces graphiques est la fonction boxplot.

Comment interpréter ce graphique ? On le comprendra mieux à partir de la figure ci-après3.
boxplot(d$heures.tv, col = grey(0.8), main = "Nombre d'heures passées devant la télé par jour",
ylab = "Heures")
abline(h = median(d$heures.tv, na.rm = TRUE), col = "navy", lty = 2)
text(1.35, median(d$heures.tv, na.rm = TRUE) + 0.15, "Médiane",
col = "navy")
Q1 <- quantile(d$heures.tv, probs = 0.25, na.rm = TRUE)
abline(h = Q1, col = "darkred")
text(1.35, Q1 + 0.15, "Q1 : premier quartile", col = "darkred",
lty = 2)
Q3 <- quantile(d$heures.tv, probs = 0.75, na.rm = TRUE)
abline(h = Q3, col = "darkred")
text(1.35, Q3 + 0.15, "Q3 : troisième quartile", col = "darkred",
lty = 2)
arrows(x0 = 0.7, y0 = quantile(d$heures.tv, probs = 0.75, na.rm = TRUE),
x1 = 0.7, y1 = quantile(d$heures.tv, probs = 0.25, na.rm = TRUE),
length = 0.1, code = 3)
text(0.7, Q1 + (Q3 - Q1)/2 + 0.15, "h", pos = 2)
mtext("L'écart inter-quartile h contient 50 % des individus",
side = 1)
abline(h = Q1 - 1.5 * (Q3 - Q1), col = "darkgreen")
text(1.35, Q1 - 1.5 * (Q3 - Q1) + 0.15, "Q1 -1.5 h", col = "darkgreen",
lty = 2)
abline(h = Q3 + 1.5 * (Q3 - Q1), col = "darkgreen")
text(1.35, Q3 + 1.5 * (Q3 - Q1) + 0.15, "Q3 +1.5 h", col = "darkgreen",
lty = 2)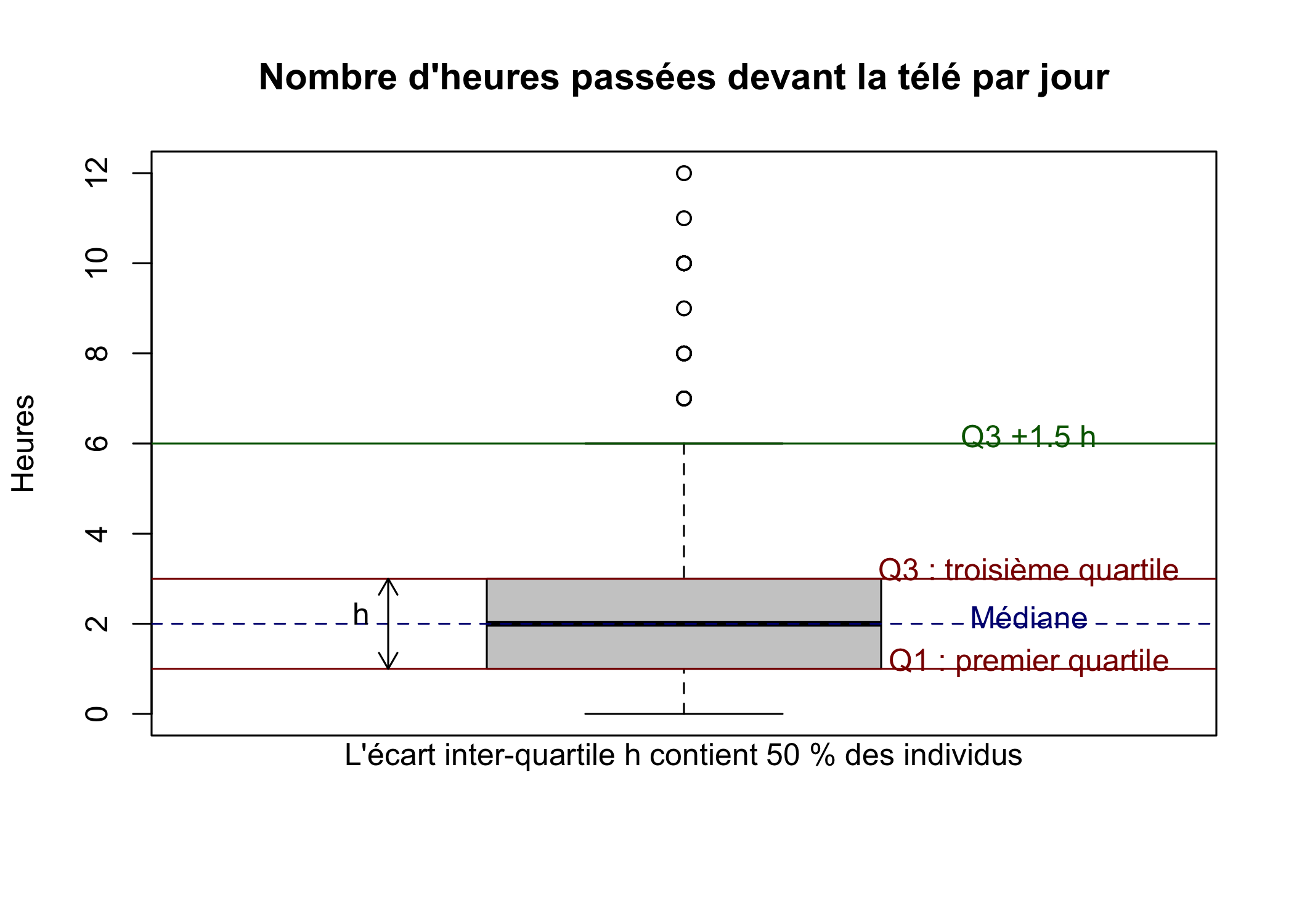
Le carré au centre du graphique est délimité par les premiers et troisième quartiles, avec la médiane représentée par une ligne plus sombre au milieu. Les « fourchettes » s’étendant de part et d’autres vont soit jusqu’à la valeur minimale ou maximale, soit jusqu’à une valeur approximativement égale au quartile le plus proche plus 1,5 fois l’écart interquartile. Les points se situant en-dehors de cette fourchette sont représentés par des petits ronds et sont généralement considérés comme des valeurs extrêmes, potentiellement aberrantes.
On peut ajouter la représentation des valeurs sur le graphique pour en faciliter la lecture avec des petits traits dessinés sur l’axe vertical (fonction rug) :
boxplot(d$heures.tv, main = "Nombre d'heures passées devant la télé par\njour",
ylab = "Heures")
rug(d$heures.tv, side = 2)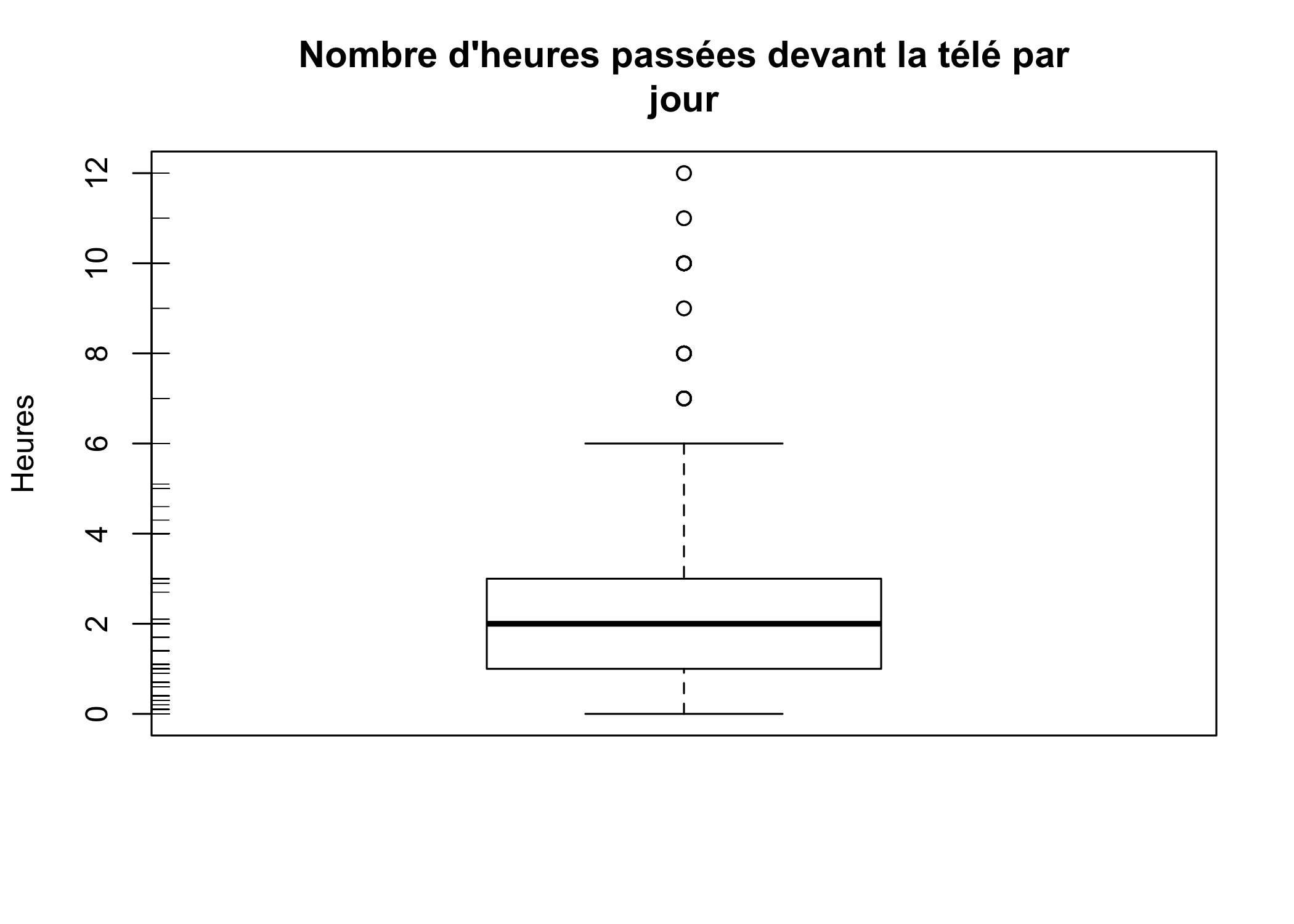
Variable qualitative
Tris à plat
La fonction la plus utilisée pour le traitement et l’analyse des variables qualitatives (variable prenant ses valeurs dans un ensemble de modalités) est sans aucun doute la fonction table, qui donne les effectifs de chaque modalité de la variable, ce qu’on appelle un tri à plat ou tableau de fréquences.
Homme Femme
899 1101 La tableau précédent nous indique que parmi nos enquêtés on trouve 899 hommes et 1101 femmes.
Quand le nombre de modalités est élevé, on peut ordonner le tri à plat selon les effectifs à l’aide de la fonction sort.
Exerce une profession Chomeur
1049 134
Etudiant, eleve Retraite
94 392
Retire des affaires Au foyer
77 171
Autre inactif
83
Retire des affaires Autre inactif
77 83
Etudiant, eleve Chomeur
94 134
Au foyer Retraite
171 392
Exerce une profession
1049
Exerce une profession Retraite
1049 392
Au foyer Chomeur
171 134
Etudiant, eleve Autre inactif
94 83
Retire des affaires
77 À noter que la fonction table exclut par défaut les non-réponses du tableau résultat. L’argument useNA de cette fonction permet de modifier ce comportement :
- avec
useNA="no"(valeur par défaut), les valeurs manquantes ne sont jamais incluses dans le tri à plat ; - avec
useNA="ifany", une colonneNAest ajoutée si des valeurs manquantes sont présentes dans les données ; - avec
useNA="always", une colonneNAest toujours ajoutée, même s’il n’y a pas de valeurs manquantes dans les données.
On peut donc utiliser :
Satisfaction Insatisfaction Equilibre <NA>
480 117 451 952 L’utilisation de summary permet également l’affichage du tri à plat et du nombre de non-réponses :
Satisfaction Insatisfaction Equilibre NA's
480 117 451 952 Pour obtenir un tableau avec la répartition en pourcentages, on peut utiliser la fonction freq de l’extension questionr4.
La colonne n donne les effectifs bruts, la colonne % la répartition en pourcentages et val% la répartition en pourcentages, données manquantes exclues. La fonction accepte plusieurs paramètres permettant d’afficher les totaux, les pourcentages cumulés, de trier selon les effectifs ou de contrôler l’affichage. Par exemple :
La colonne %cum indique ici le pourcentage cumulé, ce qui est ici une très mauvaise idée puisque pour ce type de variable cela n’a aucun sens. Les lignes du tableau résultat ont été triés par effectifs croissants, les totaux ont été ajoutés, les non-réponses exclues et les pourcentages arrondis à deux décimales.
La fonction freq est également en mesure de tenir compte des étiquettes de valeurs lorsqu’on utilise des données labellisées. Ainsi :
[2000 obs.] Région de résidence
labelled double: 4 4 4 4 4 3 3 3 3 3 ...
min: 1 - max: 4 - NAs: 0 (0%) - 4 unique values
4 value labels: [1] Nord [2] Est [3] Sud [4] Ouest
n %
[1] Nord 707 35.4
[2] Est 324 16.2
[3] Sud 407 20.3
[4] Ouest 562 28.1
Total 2000 100.0Pour plus d’informations sur la fonction freq, consultez sa page d’aide en ligne avec ?freq ou help("freq").
Représentation graphique
Pour représenter la répartition des effectifs parmi les modalités d’une variable qualitative, on a souvent tendance à utiliser des diagrammes en secteurs (camemberts). Ceci est possible sous R avec la fonction pie, mais la page d’aide de la dite fonction nous le déconseille assez vivement : les diagrammes en secteur sont en effet une mauvaise manière de présenter ce type d’information, car l’oeil humain préfère comparer des longueurs plutôt que des surfaces5.
On privilégiera donc d’autres formes de représentations, à savoir les diagrammes en bâtons et les diagrammes de Cleveland.
Les diagrammes en bâtons sont utilisés automatiquement par R lorsqu’on applique la fonction générique plot à un tri à plat obtenu avec table. On privilégiera cependant ce type de représentations pour les variables de type numérique comportant un nombre fini de valeurs. Le nombre de frères, soeurs, demi-frères et demi-soeurs est un bon exemple :
plot(table(d$freres.soeurs), main = "Nombre de frères, soeurs, demi-frères et demi-soeurs",
ylab = "Effectif")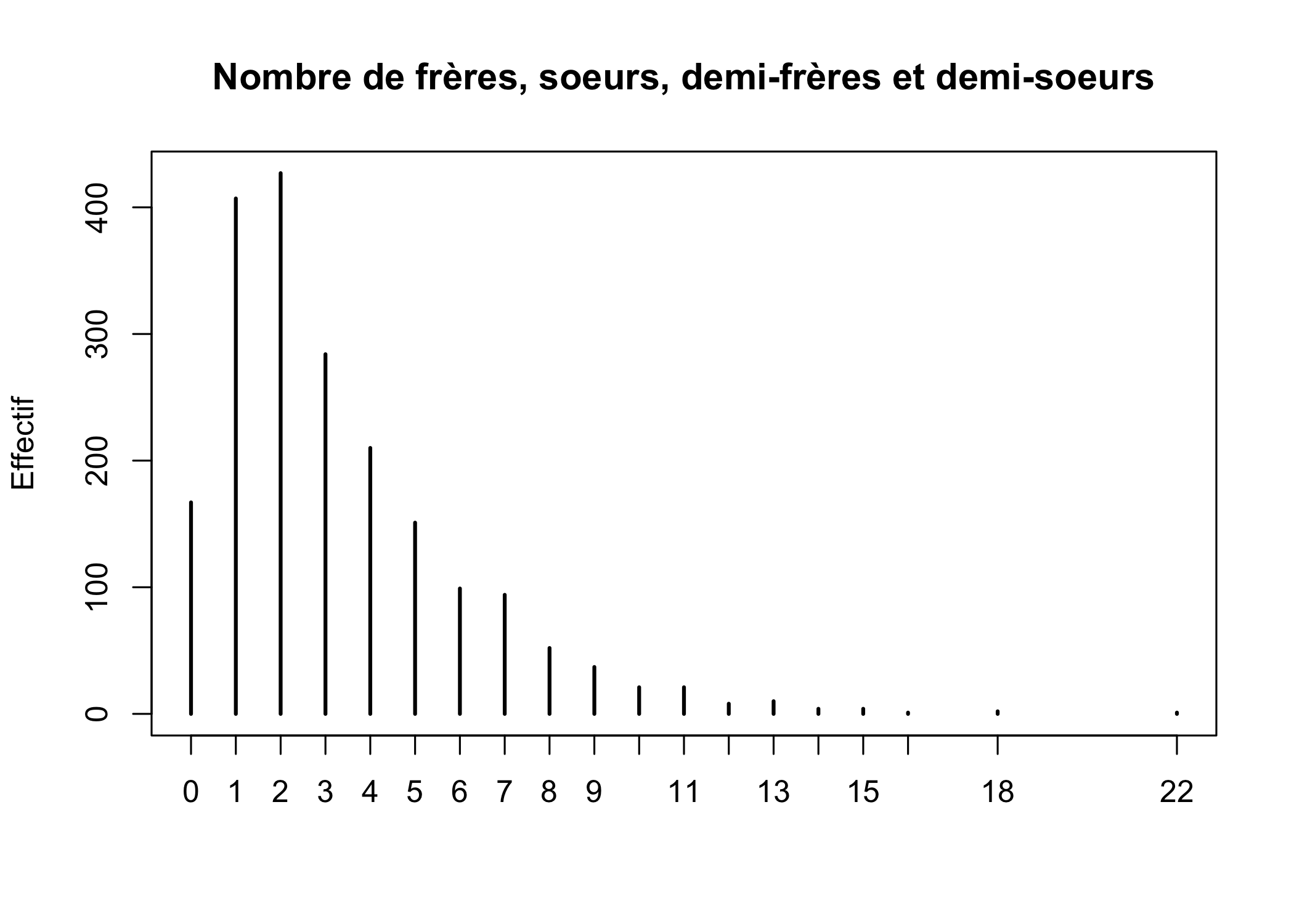
Pour les autres types de variables qualitatives, on privilégiera les diagrammes de Cleveland, obtenus avec la fonction dotchart. On doit appliquer cette fonction au tri à plat de la variable, obtenu avec table6 :
dotchart(as.matrix(table(d$clso))[, 1], main = "Sentiment d'appartenance à une classe sociale",
pch = 19)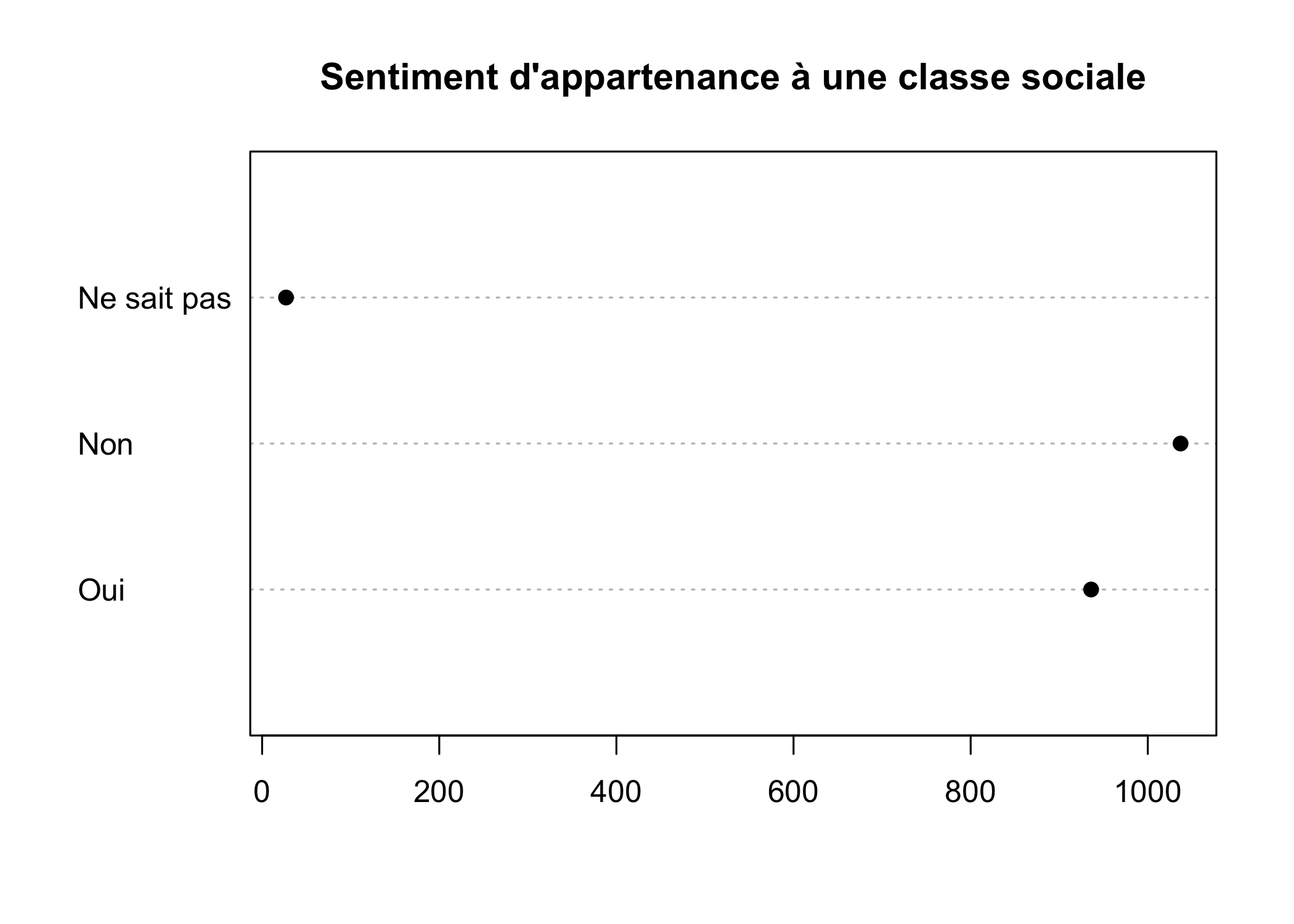
Il est possible d’entrer directement la commande suivante dans la console :
R produira bien le diagramme de Cleveland désiré mais affichera un message d’avertissement (Warning) car pour des raisons liées au fonctionnement interne de la fonction dotchart, il est attendu une matrice ou un vecteur, non un objet de type table. Pour éviter cet avertissement, il est nécessaire de faire appel à la fonction as.matrix.
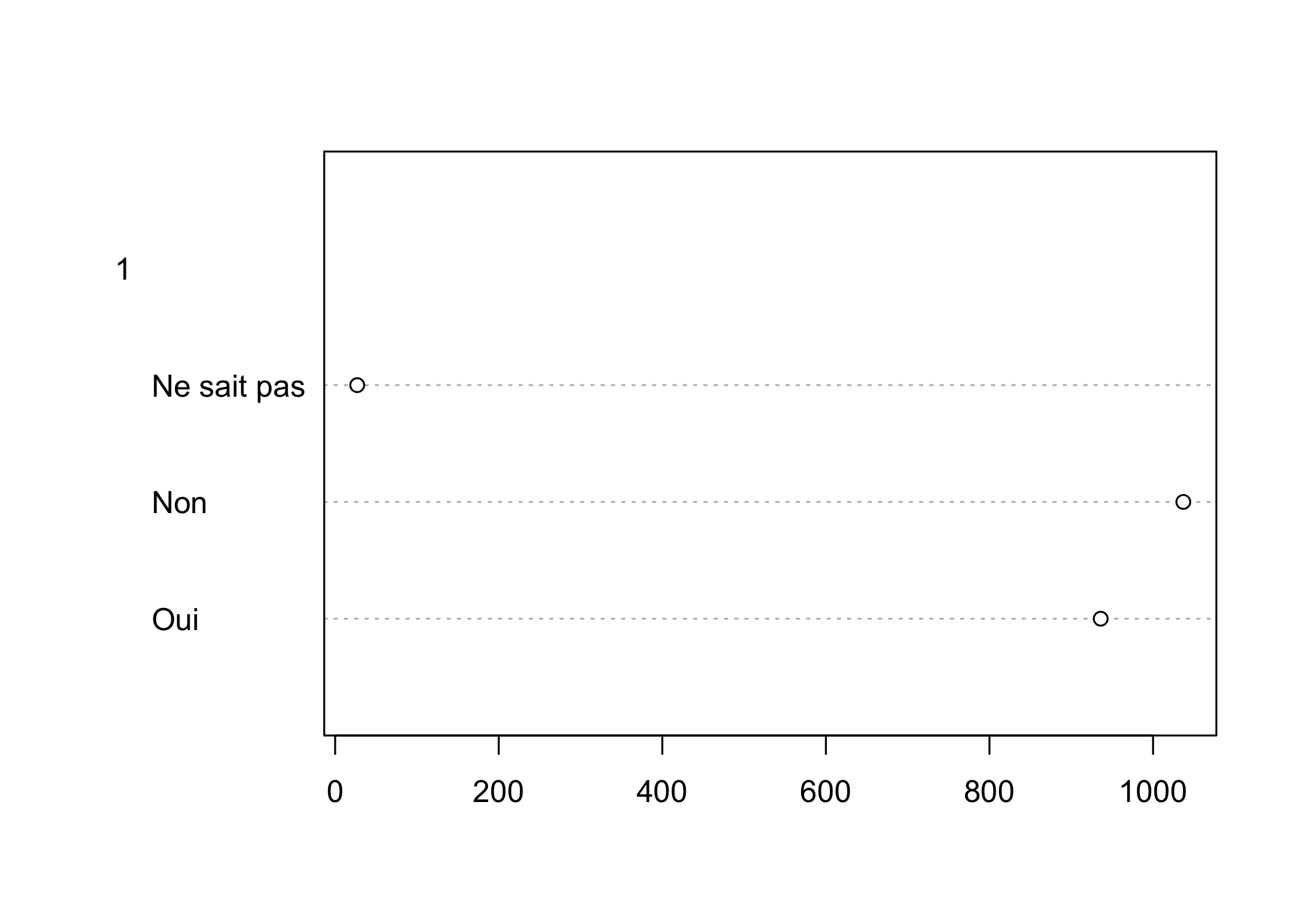
Dans le cas présent, on voit apparaître un chiffre 1 au-dessus des modalités. En fait, dotchart peut être appliqué au résultat d’un tableau croisé à deux entrées, auquel cas il présentera les résultats pour chaque colonne. Comme dans l’exemple ci-après.
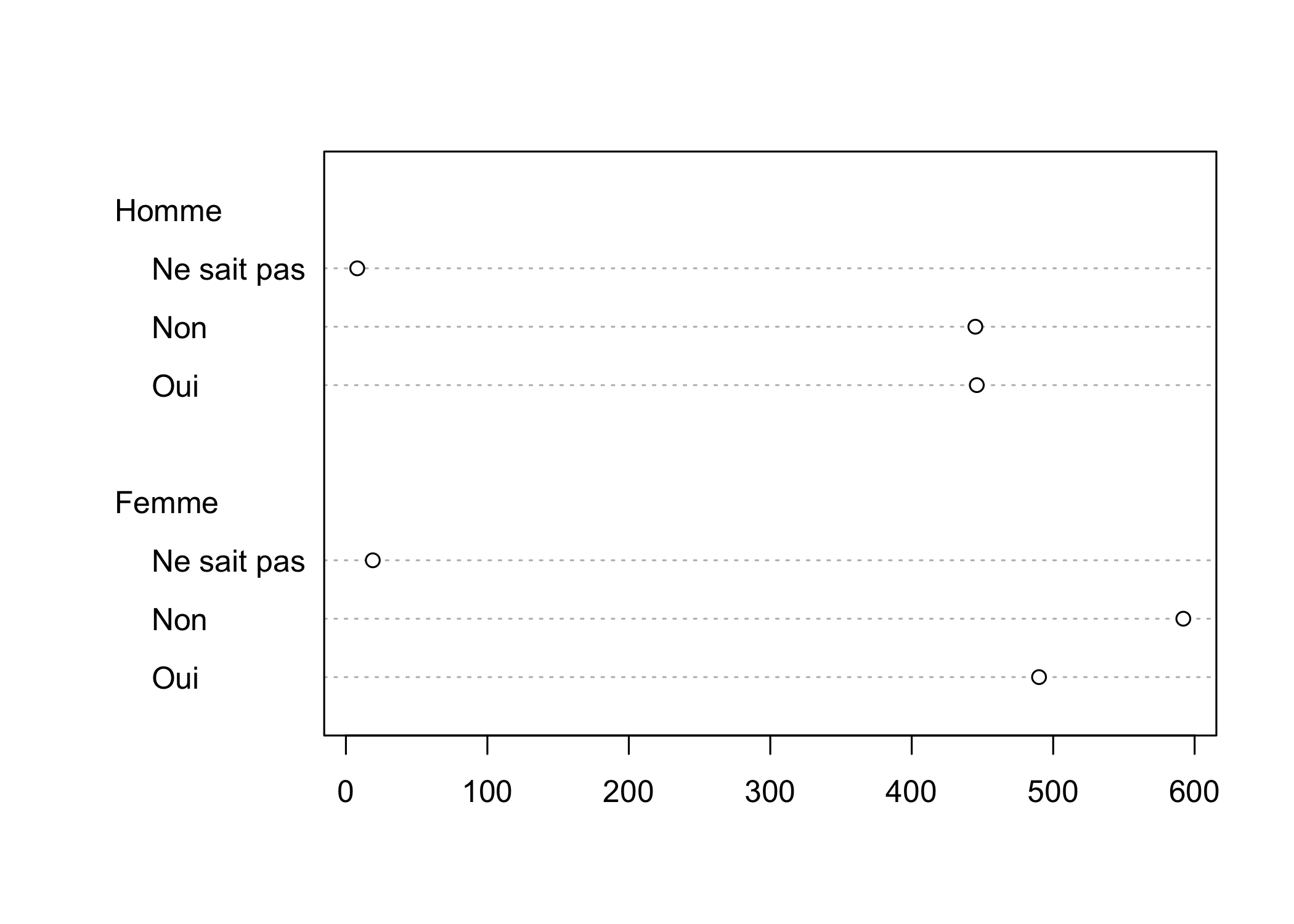
Cela ne résoud pas le problème pour notre diagramme de Cleveland issu d’un tri à plat simple. Pour bien comprendre, la fonction as.matrix a produit un objet à deux dimensions ayant une colonne et plusieurs lignes. On indiquera à R que l’on ne souhaite extraire la première colonne avec [, 1] (juste après l’appel à as.matrix). C’est ce qu’on appelle l’indexation, abordée plus en détail dans le chapitre Listes et tableaux de données.
Quand la variable comprend un grand nombre de modalités, il est préférable d’ordonner le tri à plat obtenu à l’aide de la fonction sort :
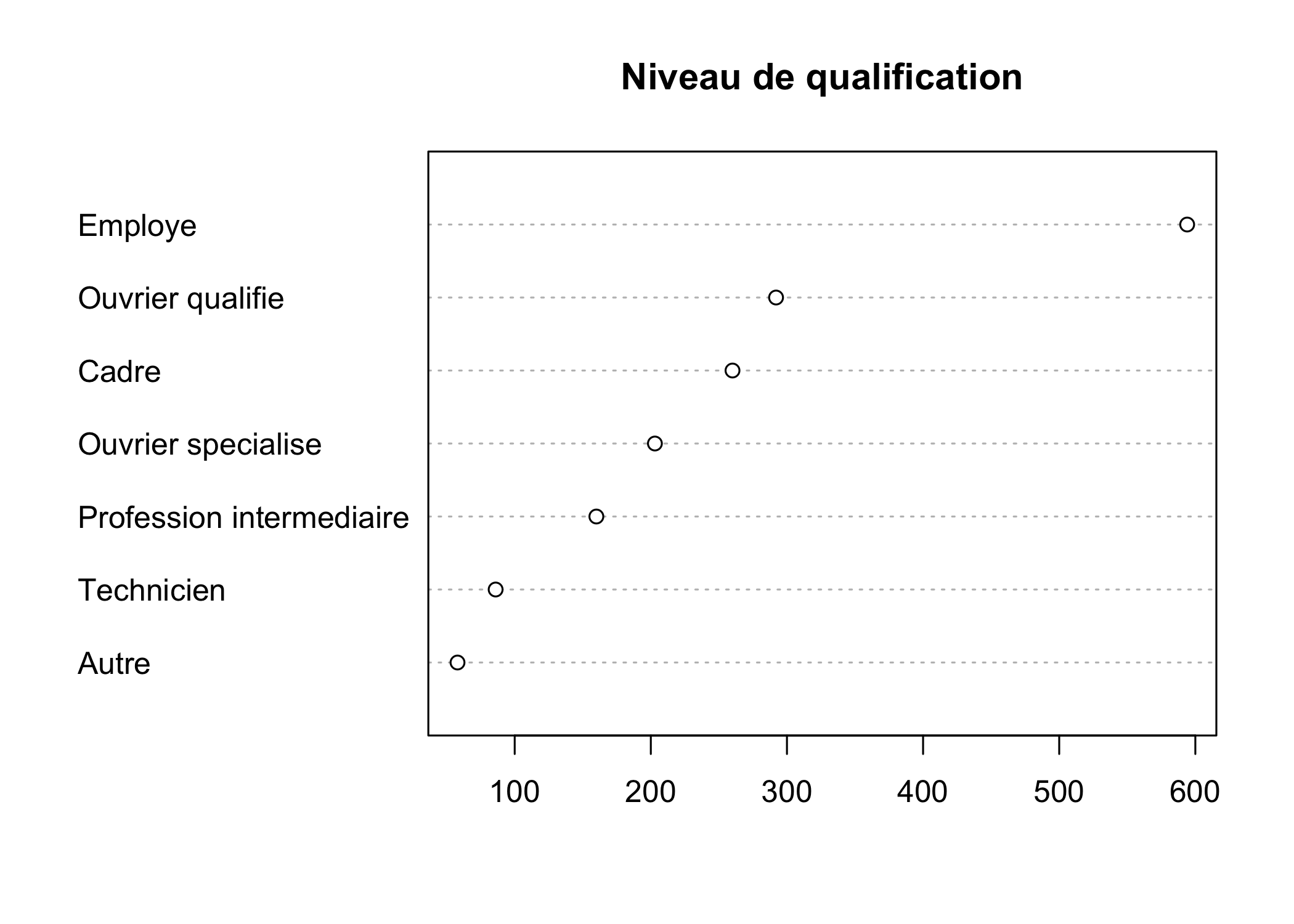
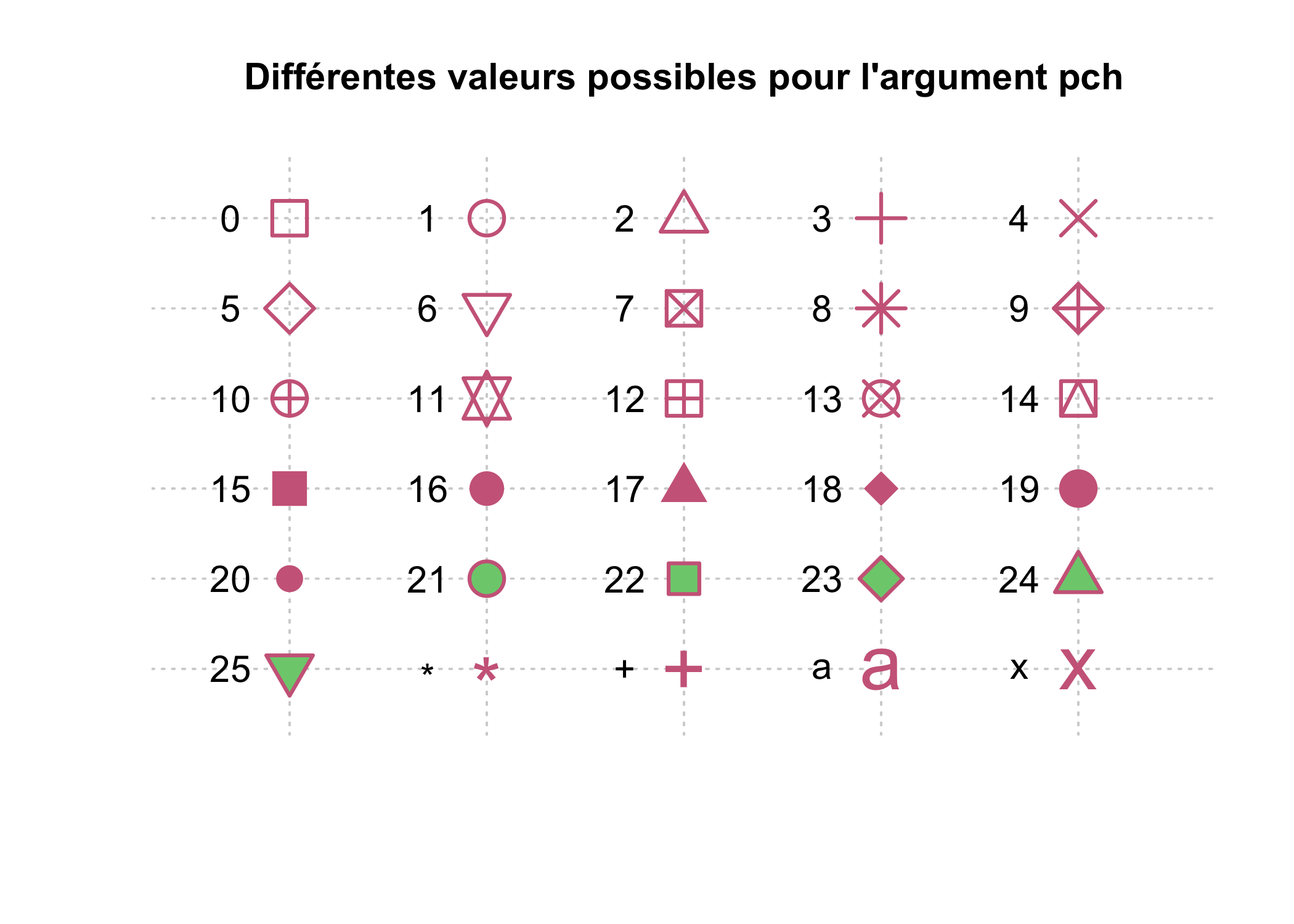
L’agument pch, qui est utilisé par la plupart des graphiques de type points, permet de spécifier le symbole à utiliser. Il peut prendre soit un nombre entier compris entre 0 et 25, soit un charactère textuel (voir ci-dessous).
Exporter les graphiques obtenus
L’export de graphiques est très facile avec RStudio. Lorsque l’on créé un graphique, ce dernier est affiché sous l’onglet Plots dans le quadrant inférieur droit. Il suffit de cliquer sur Export pour avoir accès à trois options différentes :
- Save as image pour sauvegarder le graphique en tant que fichier image ;
- Save as PDF pour sauvegarder le graphique dans un fichier PDF ;
- Copy to Clipboard pour copier le graphique dans le presse-papier (et pouvoir ainsi le coller ensuite dans un document Word par exemple).
Pour une présentation détaillée de l’export de graphiques avec RStudio, ainsi que pour connaître les commandes R permettant d’exporter des graphiques via un script, on pourra se référer au chapitre dédié.
Il existe un grand nombre de couleurs prédéfinies dans R. On peut récupérer leur liste en utilisant la fonction
colorsen tapant simplementcolors()dans la console, ou en consultant le document suivant : http://www.stat.columbia.edu/~tzheng/files/Rcolor.pdf.↩Le code ayant servi à générer cette figure est une copie quasi conforme de celui présenté dans l’excellent document de Jean Lobry sur les graphiques de base avec R, téléchargeable sur le site du Pôle bioinformatique lyonnais : http://pbil.univ-lyon1.fr/R/pdf/lang04.pdf.↩
En l’absence de l’extension
questionr, on pourra se rabattre sur la fonctionprop.tableavec la commande suivante :prop.table(table(d$qualif)).↩Voir en particulier https://www.data-to-viz.com/caveat/pie.html pour un exemple concret.↩
Pour des raisons liées au fonctionnement interne de la fonction
dotchart, on doit transformer le tri à plat en matrice, d’où l’appel à la fonctionas.matrix.↩
