ou modèles à effets aléatoires permettent de prendre en considération ce type d’information et de généraliser l’approche déjà connue pour l’estimation des paramètres d’un modèle de régression linéaire classique (pour observations indépendantes).

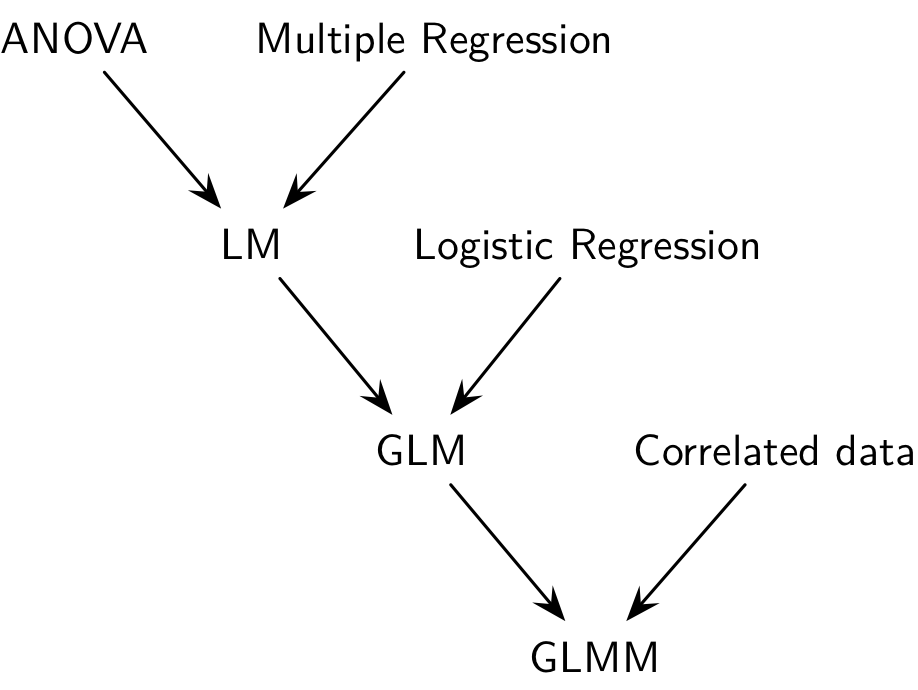Modèles de régression Typologie des modèles de régression

Modèles mixtes (GLMM)

Par rapport au modèle linéaire (généralisé) classique, les modèles mixtes (GLMM dans la littérature anglo-saxonne) considèrent, en plus des effets fixes, des effets aléatoires qui permettent de refléter la corrélation entre les unités statistiques. Ce type de données en cluster s’observe lorsque des unités statistiques sont groupées ensemble (étudiants dans des écoles), en raison d’une corrélation intra-unité (données longitudinales) ou un mélange des deux (performance mesurée au cours du temps pour différents groupes de sujets).

On rattache ce type de modèle aux approches conditionnelles, par opposition aux approches marginales telles que les GLS ou les GEE, décrites dans la deuxième partie de ce chapitre. Les modèles mixtes ne se limitent pas à un seul niveau de cluster, et il peut exister une hiérarchie de clusters imbriqués les uns dans les autres, d’où l’appelation de modèles hiérarchiques dans certains cas de figure.

En ce qui concerne les effets fixes versus aléatoires, il existe peu de définition consensuelle, mais on peut considérer le schéma suivant pour décider si un effet doit être considéré comme fixe ou aléatoire :

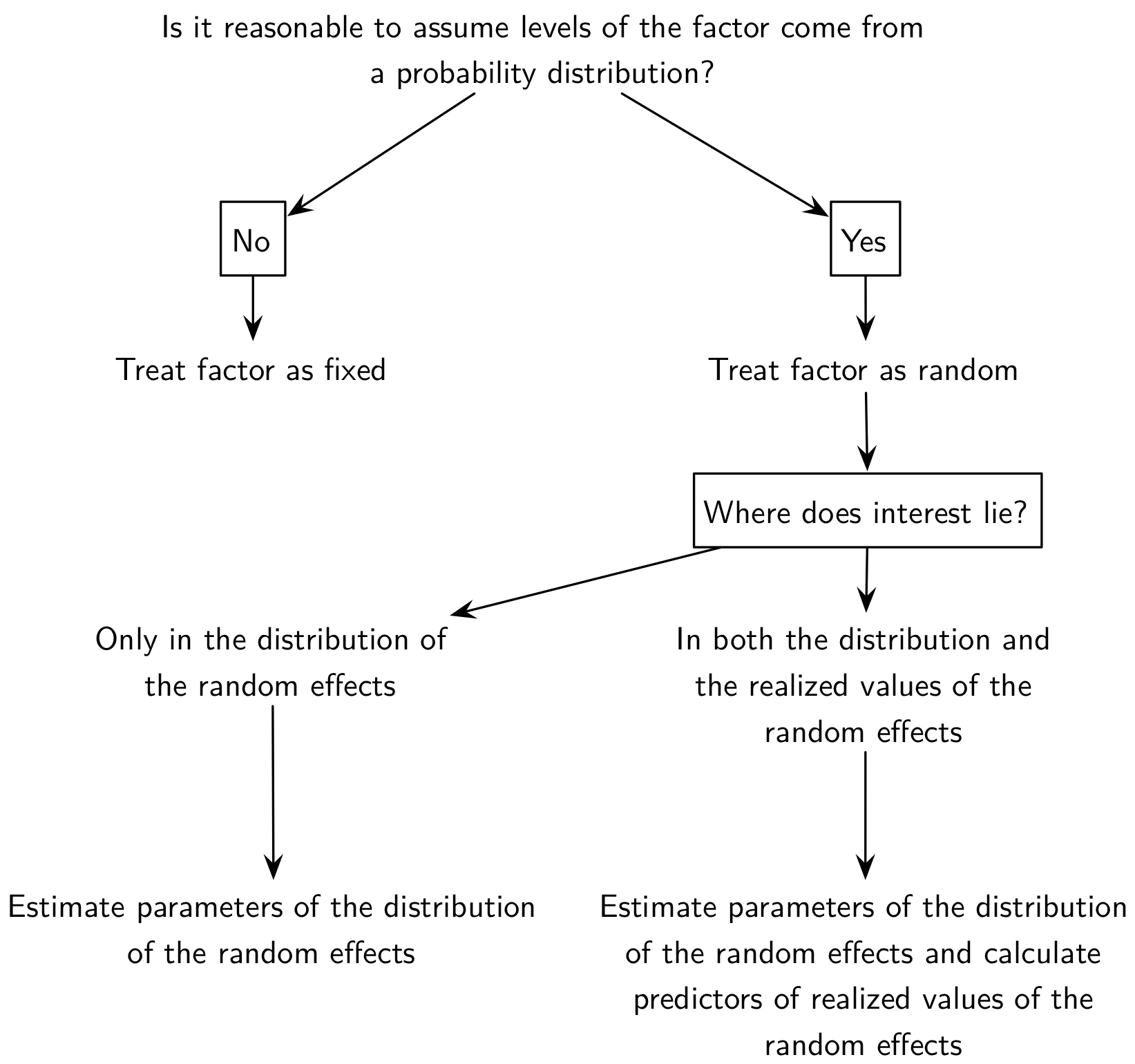Modèles de régression Schéma décisionnel pour définir un effet

L’analyse des données corrélées ou appariées permet de mettre en lumière l’importance de tenir compte de la structure de corrélation intra-unité. Voici l’exemple célèbre des données sur le sommeil utilisé par W. Gosset pour présenter son test de Student :

t.test(extra ~ group, data=sleep)
t.test(extra ~ group, data=sleep, paired = TRUE)

Le résultat du test dans le premier cas de figure, qui ignore complètement l’appariement, se révèle non significatif alors que la prise en compte de l’appariement indique qu’il existe bien une différence significative dans le gain de sommeil selon le type d’hypnotique administré.

Ignorer la corrélation intra-unité résulte en test généralement moins puissant sur le plan statistique. On sait que dans le cas où deux variables aléatoires, X1 et X2, ne sont pas indépendantes, la variance de leur différence vaut :


Var(X1 − X2) = Var(X1) + Var(X2) − 2Cov(X1, X2).

Considérer que Cov(X1, X2) = 0 revient à sur-estimer la variance de la différence, dans la mesure où Cov(X1, X2) est généralement positive, soulignant le fait que les individus ayant un niveau plus élevé sur le premier niveau de la variable explicative ont généralement un niveau plus élevé que les autres sur le second niveau. On peut visualiser cette tendance très clairement avec les données “sleep” :

library(lattice)
library(gridExtra)
#lattice.options(default.theme=brewer.theme)
trellis.par.set(strip.background = list(col = 'transparent'))
data(sleep)
xyplot(extra ~ group, data=sleep, groups=ID, type="l")

Les données “sleep” de Student

Cas de l’ANOVA à mesures répétées

Voici des données concernant l’excès de graisse dans les scelles suite à une défaillance des enzymes de digestion dans l’intestin. Des suppléments en enzyme pancréatique permettent de corriger ce problème, la question étant de déterminer quel est le meilleur mode d’administration (tablette, capsule, enrobé) :

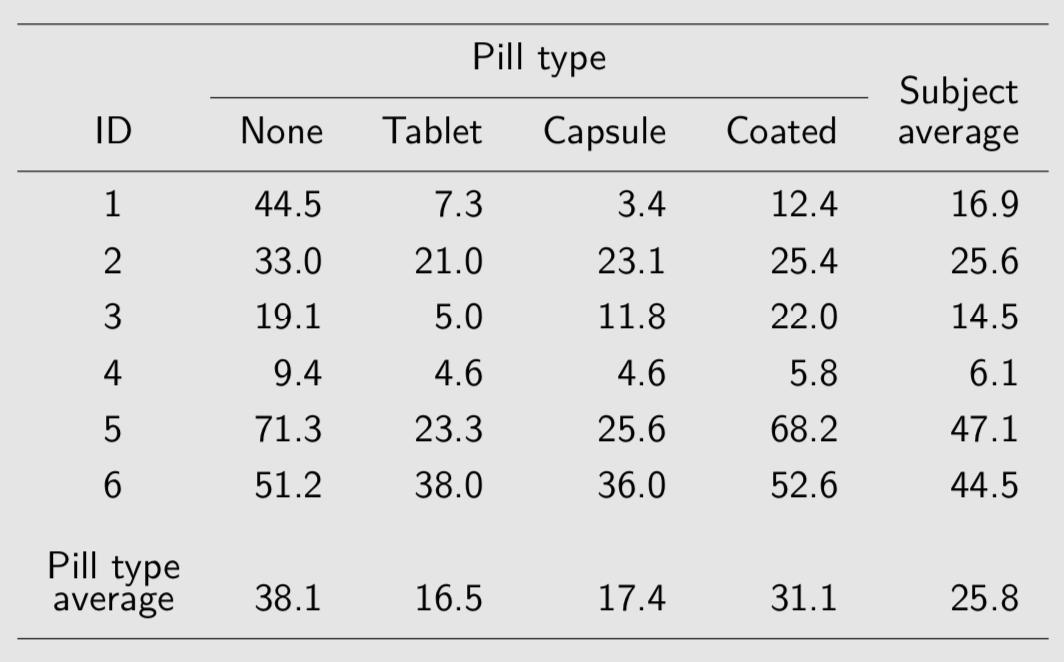
Fecal fat study

Fecal fat study

Il n’y a qu’un seul prédicteur, le type de comprimé, qui est attaché au sujet et à la période d’administration dans le temps (répétition sur un même sujet). On dispose de plusieurs manières de décomposer la variance totale :

```{r} fat 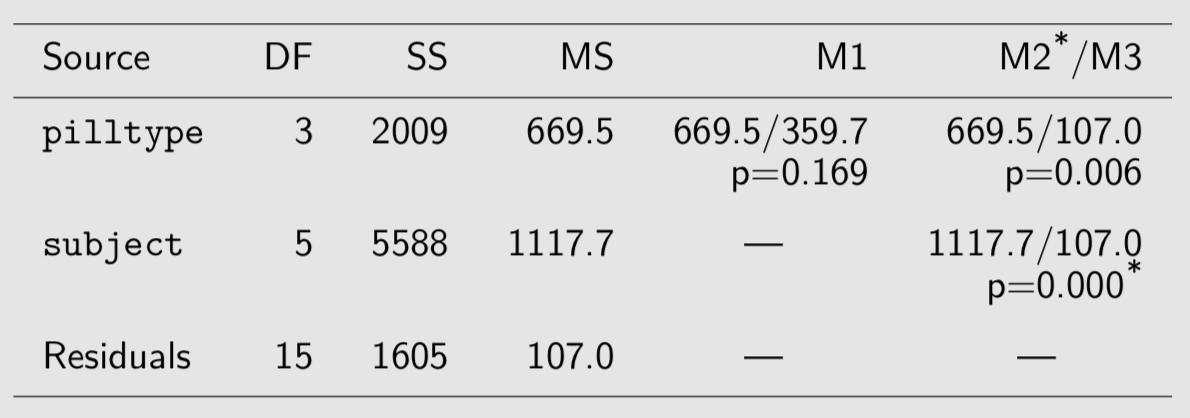Fecal fat study

Le premier modèle, qui suppose les observations indépendantes, ne supprime pas la variance entre sujets (presque 78~% de la variance résiduelle). Les deux modèles suivants, M2 et M3, incorpore chacun des effets spécifiques aux sujets :


$$ y_{ij} = \mu + \text{subject}_i + \text{pilltype}_j + \varepsilon_{ij},\quad \varepsilon_{ij}\sim{\cal N}(0,\sigma_{\varepsilon}^2). $$

Dans le troisième modèle (M3), on suppose de plus que $\text{subject}_i\sim{\cal N}(0,\sigma_{s}^2)$, indépendant de εij. L’inclusion de termes aléatoires sujet-spécifique permet de modéliser différents types de corrélation intra-unité au niveau de la variable réponse. Considérons la corrélation entre des mesures prises successivement chez le même individu. On sait que :


$$ \text{Cor}(y_{ij},y_{ik})=\frac{\text{Cov}(y_{ij},y_{ik})}{\sqrt{\text{Var}(y_{ij})}. $$

Puisque μ et pilltype sont fixes, et que εij ⊥ subjecti, on a donc :


$$ \begin{align} \text{Cov}(y_{ij},y_{ik}) & = \text{Cov}(subject_i,subject_i) \cr & = \text{Var}(subject_i) \cr & = \sigma_{s}^2, \end{align} $$

et les composantes de variance résultent du fait que Var(yij) = Var(subjecti) + Var(εij) = σs2 + σε2, que l’on suppose vrai pour toutes les observations. De sorte qu’on arrive à la quantité que nous recherchions, à savoir la corrélation entre deux mesures, j et k, prises chez le même individu i :


$$ \text{Cor}(y_{ij},y_{ik})=\frac{\sigma_{s}^2}{\sigma_{s}^2+\sigma_{\varepsilon}^2}. $$

Cette valeur reflète la proportion de la variance totale qui est dûe aux individus eux-mêmes. On la dénomme également corrélation intraclasse, ρ, et elle permet de quantifier le degré de proximité entre les observations de différents individus (on parle également de similarité intra-cluster) :

  • la variabilité entre sujets augmente ou diminue simultanément toutes les observations d’un même sujet ;
  • la structure de variance-covariance du modèle ci-dessus est appelée “symétrie composée”.

On retrouve alors l’égalité σ2 = σs2 + σε2, qui revient à :


$$ \begin{bmatrix} \sigma_{s}^2+\sigma_{\varepsilon}^2 & \sigma_{s}^2 & \sigma_{s}^2 & \sigma_{s}^2 \cr \sigma_{s}^2 & \sigma_{s}^2+\sigma_{\varepsilon}^2 & \sigma_{s}^2 & \sigma_{s}^2 \cr \sigma_{s}^2 & \sigma_{s}^2 & \sigma_{s}^2+\sigma_{\varepsilon}^2 & \sigma_{s}^2 \cr \sigma_{s}^2 & \sigma_{s}^2 & \sigma_{s}^2 & \sigma_{s}^2+\sigma_{\varepsilon}^2 \cr \end{bmatrix} = \sigma^2 \begin{bmatrix} 1 & \rho & \dots & \rho \cr \rho & 1 & & \rho \cr \vdots & & \ddots & \vdots \cr \rho & \rho & \dots & 1 \cr \end{bmatrix} $$

L’estimation de ρ passe par l’observation suivante : les observations prises sur un même sujet sont modélisés via leur effet aléatoire (sujet-spécifique) partagé. En utilisant le modèle à intercept aléatoire considéré plus haut, il est possible d’estimer ρ à l’aide du package nlme :

```{r} library(nlme) lme.fit

```{r} fat$pred Valeurs observées et prédites pour l’étude “fecal fat”

Quelques remarques :

  • pour un dessin expérimental équilibré, la variance résiduelle d’une ANOVA à effet intra (cas des mesures répétées) et celle d’un modèle à intercept aléatoire sont identiques (l’estimateur REML est équivalent au carré moyen de l’ANOVA) ; de même les effets liés au type de comprimé seront identiques aux moyennes marginales ;
  • le test de la significativité des effets fixes peut être réalisé à l’aide de l’ANOVA (tests F) ou par comparaison de modèles emboîtés ; dans ce dernier cas, il est nécessaire d’estimer les paramètres du modèle mixte par maximum de vraismeblance et non par REML puisque les modèles emboîtés vont inclure des effets fixes différents :

```{r} anova(lme.fit) lme.fit Average reaction time per day for subjects in a sleep deprivation study. On day 0 the subjects had their normal amount of sleep. Starting that night they were restricted to 3 hours of sleep per night. The observations represent the average reaction time on a series of tests given each day to each subject.

detach(package:nlme)
library(lme4)
data(sleepstudy)
xyplot(Reaction ~ Days | Subject, data = sleepstudy,
       layout = c(9,2), type=c("g", "p", "r"),
       index.cond = function(x,y) coef(lm(y ~ x))[1],
       xlab = "Days of sleep deprivation",
       ylab = "Average reaction time (ms)")

Temps de réaction en fonction de la durée de privation de sommeil

Considérons dans un premier temps de simples régressions linéaires pour chaque sujet :

```{r} reg.subj

```{r} intcpt.dens Droites de régression individuelles

On voit clairement que les sujets présentent des profils d’évolution différents et l’équation de la droite de régression globale est : ỹ = 251.4 + 10.5x.. La question qui se pose est : dans quelle mesure cette équation capture t-elle la tendance observée entre les différents sujets ?

Les estimations par moindres carrés sujet-spécifique sont bel et bien correctes mais l’erreur standard des paramètres de ces modèles sont biaisés puisque l’on suppose l’indépendance des observations. Les prédictions seront également incorrectes.

Voici quelques modèles à effets aléatoires plausibles pour ce type de données :

  • Random-intercept model : Reaction ~ Days + (1 | Subject)
  • Random-intercept and slope model : Reaction ~ Days + (Days | Subject)
  • Uncorrelated random effects (intercept and slope) : Reaction ~ Days + (1 | Subject) + (0 + Days | Subject)

```{r} lme.mod1

```{r} df Valeurs prédites par les modèles

Les valeurs prédites d’un modèle mixte peuvent également être vues comme des estimateurs “shrinkage”. Dans les cas les plus simples, le coefficient de régularisation revient à :


$$ \tau = \frac{\sigma_u^2}{\sigma_u^2+\sigma_{\varepsilon}^2/n_i}, $$

où ni désigne la taille du cluster i. Dans le cas présent, τ = 37.12/(37.12 + 31.02/10) = 0.935. Il y aura peu de régularisation lorsque les unités statistiques sont très différentes ou que les mesures sont peu précises, ou dans le cas des grands échantillons.

    Random effects:                                    Reaction Days Subject     pred
    Groups   Name        Variance Std.Dev.        1   249.5600    0     308 292.1888
    Subject  (Intercept) 1378.18  37.124          2   258.7047    1     308 302.6561
    Residual              960.46  30.991          3   250.8006    2     308 313.1234
    Number of obs: 180, groups: Subject, 18        4   321.4398    3     308 323.5907
                                                ...
    Fixed effects:                                 177 334.4818    6     372 332.3246
                Estimate Std. Error t value        178 343.2199    7     372 342.7919
    (Intercept) 251.4051     9.7459   25.80        179 369.1417    8     372 353.2591
    Days         10.4673     0.8042   13.02        180 364.1236    9     372 363.7264

```{r} intcpt.dens2 Valeurs prédites et effet de régularisation

Cas des données corrélées discrètes

Approche GEE

Le cas des données discrètes pose en plus le problème du choix de la distribution pour la variable réponse (ou les erreurs). Une distribution binomiale ou multinomiale convient mieux aux cas où la variable modélisée correspond à un choix binaire ou à plus de deux catégories de réponse. De plus, le choix de la stratégie de modélisation influence également les conclusions que l’on peut tirer d’une étude. Comme on l’a vu plus haut, les modèles linéaires mixtes généralisés permettent d’estimer les paramètres sujet-spécifiques d’un modèle de régression en considérant des effets fixes et/ou aléatoires, éventuellement en considérant différentes structures de corrélation. Une alternative consiste à modéliser directement les effets moyens des facteurs fixes, sans se soucier des effets individuels, en supposant toutefois une matrice de corrélation de travail qui permette de rendre compte de la corrélation intra-unité. Cette approche est connue sous le terme Équations d’estimation généralisées (GEE dans la littérature anglo-saxonne).

En ce qui concerne la matrice de corrélation de travail, voici 4 solutions qui peuvent constituer notre modèle de variance. Le premier cas correspond à une matrice d’indépendance (ind), où toutes les observations sont indépendantes les unes des autres :


$$ \begin{pmatrix} 1 & 0 & \cdots & 0 \cr 0 & 1 & \cdots & 0 \cr \vdots & \vdots & \ddots & \vdots \cr 0 & 0 & \cdots & 1 \end{pmatrix} $$

On peut également considérer le cas d’une structure de corrélation symétrique ou échangeable (exch), telle que celle assumée dans une ANOVA à mesures répétées (cf. hypothèse de symétrie composée, ou sphéricité), où ρ désigne la corrélation intraclasse :


$$ \begin{pmatrix} 1 & \rho & \cdots & \rho \cr \rho & 1 & \cdots & \rho \cr \vdots & \vdots & \ddots & \vdots \cr \rho & \rho & \cdots & 1 \end{pmatrix} $$

Une structure plus libérale consiste à supposer que les corrélations intra-unités sont libres de varier d’une unité à l’autre, et sont donc non structurées (uns) :


$$ \begin{pmatrix} 1 & \rho*{1,2} & \cdots & \rho*{1,t} \cr \rho*{1,2} & 1 & \cdots & \rho*{2,t} \cr \vdots & \vdots & \ddots & \vdots \cr \rho*{1,t} & \rho*{2,t} & \cdots & 1 \end{pmatrix} $$

Enfin, il est également possible, surtout dans le cas des données temporelles, de considérer une structure de corrélation sérielle auto-régressive (ar) :


$$ \begin{pmatrix} 1 & \rho & \cdots & \rho^{t-1} \cr \rho & 1 & \cdots & \rho^{t-2} \cr \vdots & \vdots & \ddots & \vdots \cr \rho^{t-1} & \rho^{t-2} & \cdots & 1 \end{pmatrix} $$

Comment choisir une bonne matrice de corrélation de travail pour notre modèle GEE ? En règle générale, on testera le modèle avec deux matrices de corrélation (p.ex. exch et uns) pour vérifier si l’une des deux améliore sensiblement la qualité de l’ajustement ou si une structure particulière est bien en accord avec notre modèle de variance présupposé. Voici également quelques critères globaux permettant de choisir l’une ou l’autre des structures de corrélation possibles :

  • non structurée : peu d’unités par cluster, dessin expérimental équilibré ;
  • échangeable : les unités d’un même cluster n’ont pas d’ordre particulier ;
  • auto-régressive : afin de rendre compte d’une réponse variant avec le temps ;
  • indépendante : lorsque le nombre de clusters est faible.

Reste la question d’évaluer dans quelle mesure la matrice de corrélation retenue est appropriée, ce qui revient à formuler un test de spécification. La sensibilité à la mauvaise spécification de la matrice de corrélation se reflètera directement dans la précision des paramètres estimés, ou de manière équivalente au niveau de l’amplitude de leurs erreurs standard. Les estimateurs de variance peuvent de surcroît être de type “model-based” (pratique dans le cas d’un faible nombre de clusters, le cas échéant il est toujours possible d’utiliser un estimateur “jacknife”) ou empiriques (on parle d’estimateurs “sandwich”, et ils sont asymptotiquement sans bias). Mais on retiendra que même si la matrice de corrélation est mal spécifiée, le modèle GEE fournit des résultats valides sous réserve que l’estimateur de variance sandwich soit utilisé.

Voici une petite illustration sur des données tirées d’une étude sur l’effet de la pollution de l’air sur la capacité respiratoires chez 537 enfants agés de 7 à 10 ans. Le fait que la mère fume et le temps constituent les prédicteurs d’intérêt, et la variable réponse est la présence d’un symptôme asthmatique (respiration sifflante). Les données collectées sont résumées dans le tableau suivant :

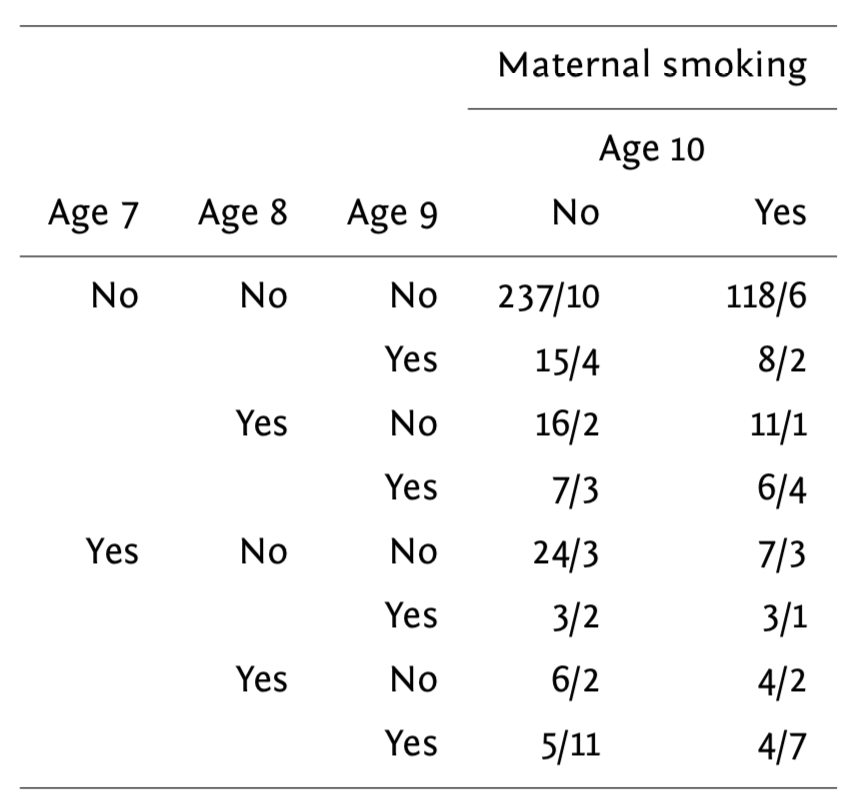
Tableau des résultats sur l’étude wheeziness

Tableau des résultats sur l’étude wheeziness

Le modèle considéré s’écrit :

$$

$$

et on parlera de “mean model” pour désigner un tel modèle dans lequel on s’intéresse à l’effet moyen (ici l’odds-ratio pour le status respiratoire) en fonction des prédicteurs, considérés à effets fixes dans ce modèle. Notons que ce modèle incorpore également un terme d’interaction (β3).

Il est également nécessaire de spécifier la fonction variance. Dans ce cas précis, on choisira 𝕍(μ) = ϕμ ⋅ (1 − μ), avec ϕ = 1 pour le paramètre d’échelle. On ne fait aucune hypothèse sur la distribution des observations.

Voici les données :

library(geepack)
data(ohio)
head(ohio, n=8)
length(unique(ohio$id))

```{r} smoke.yes Fréquence des symptômes respiratoires en fonction du groupe d’âge et du status fumeur de la mère

Et voici pour l’application numérique avec le package geepack. Le premier modèle que nous considérerons figure une matrice de corrélation de travail de type symétrique :

```{r} fm

```{r} gee.fit.exch3 Probabilités marginales prédites pour les deux groupes au cours du temps

Approche GLMM

On peut comparer les résultats précédents avec ceux que l’on obtiendrait via une approche par modèle linéaire mixte. La syntaxe est la suivante :

```{r} library(lme4) fit.glmm

A

ACM

ACP

AFC

âge

âge atteint dans l’année

âge au dernier anniversaire

âge exact

AIC

aide

aide en ligne

Akaike Information Criterion

aléatoire, échantillonnage

aléatoire, effet

analyse de séquences

analyse de survie

analyse des biographies

analyse des correspondances multiples

analyse en composante principale

analyse factorielle

analyse factorielle avec données mixtes

analyse factorielle des correspondances

ANOVA

appariement optimal

arbre de classification

argument

argument nommé

argument non nommé

assignation par indexation

assignation, opérateur

attribut

autocomplétion

B

barres cumulées, diagramme en

barres cumulées, graphique

barres, diagramme en

bâton, diagramme

bâtons, diagramme en

Bayesian Highest Density Intervals

binaire, régression logistique

biographie, analyse

bitmap

boîte à moustache

boîte à moustaches

booléenne, valeur

booléenne, variable

boxplot

C

CAH

camembert, graphique

caractères, chaîne

catégorielle, variable

censure à droite

cercle de corrélation

chaîne de caractères

character

chemin relatif

Chi², distance

Chi², résidus

Chi², test

chunk

classe de valeurs

classe, homogénéité

classes latentes, modèle mixte

classification ascendante hiérarchique

classification, arbre

Cleveland, diagramme

cluster

coefficient de contingence de Cramer

coefficient de corrélation

coefficient, modèle

coefficients du modèle

colinéarité

coloration syntaxique

commentaire

comparaison de courbes de survie (test du logrank)

comparaison de médianes, test

comparaison de moyennes

comparaison de proportions, test

comparaison, opérateur

Comprehensive R Archive Network

condition, indexation

confusion, matrice

console

corrélation

corrélation, cercle

corrélation, coefficient

corrélation, matrice de

correspondances, analyse factorielle

couleur

couleur, palette

courbe de densité

Cox, modèle

Cramer, coefficient de contingence

CRAN

croisé, tableau

CSV, fichier

D

data frame

data.frame

date, variable

dendrogramme

densité, courbe de

densité, estimation locale

descriptive, statistique

design

diagramme de Cleveland

diagramme de Lexis

diagramme en barres

diagramme en barres cumulées

diagramme en bâtons

diagramme en secteur

distance

distance de Gower

distance du Chi²

distance du Phi²

distance, matrice

distribution

donnée labelissée

données pondérées

données, exporter

données, tableau

droite de régression

droite, censure

E

écart interquartile

écart-type

échantillonnage aléatoire simple

échantillonnage équiprobable

échantillonnage par grappes

échantillonnage stratifié

échantillonnage, plan

éditeur de script

effet aléatoire

effet d’interaction

empirical cumulative distribution function

entier

entier, nombre

entropie transversale

environnement de développement

environnement de travail

équiprobable, échantillonnage

erreurs

estimation locale de densité

estimation par noyau

étendue

étiquette de valeur

étiquette de variable

étiquettes de valeurs

event history analysis

exact, âge

explicative, variable

export de graphiques

exporter des données

expression régulière

extension

F

facteur

facteurs d’inflation de la variance

factor

factoriel, plan

factorielle, analyse

fichier CSV

fichier de commandes

fichier texte

fichiers Shapefile

Fisher, test exact

FIV

fonction

fonction de répartition empirique

formule

fréquence, tableau

fusion

fusion de tables

G

GEE, modèle

gestionnaire de versions

Gower, distance

Gower, indice de similarité

graphique de pirates

graphique en mosaïque

graphique en violon

graphique, export

grappe, échantillonnage

H

hazard ratio

hazard ratio (HR)

HDI

histogramme

historique des commandes

homogénéité des classes

I

image bitmap

image matricielle

image vectorielle

indépendance

indertie, perte relative

index plots

indexation

indexation bidimensionnelle

indexation directe

indexation par condition

indexation par nom

indexation par position

indexation, assignation

indice de similarité

indice de similarité de Gower

inertie

inertie, saut

installation

integer

interaction

intercept

interface

interquartilen écart

intervalle de confiance

intervalle de confiance d’un odds ratio

intervalle de confiance d’une moyenne

intervalle de confiance d’une proportion

invite de commande

K

Kaplan-Meier

L

labelled data

labellisé, vecteur

labellisée, donnée

labellisée, variable

latente, modèle mixte à classes latentes

LCS

level, factor

Lexis, diagramme

libre, logiciel

life course analysis

linéaire, régression

liste

logical

logiciel libre

logique, opérateur

logique, valeur

logistique, régression

logrank, test (comparaison de courbes de survie)

loi normale

Longuest Common Subsequence

M

Mann-Whitney, test

manquante, valeur

Markdown

matching, optimal

matrice de confusion

matrice de corrélation

matrice de distances

maximum

médiane

médiane, test de comparaison

métadonnée

méthode de Ward

minimum

mise à jour, R

mixte, modèle

mixte, modèle mixte à classes latentes

mixtes, analyse factorielle avec données

modalité

modalité de référence

modalité, facteur

modèle à effets aléatoires

modèle de Cox

modèle GEE

modèle linéaire généralisé

modèle mixte

modèle, coefficients

modèle, résidus

mosaïque, graphique

moustaches, boîte

moyenne

moyenne, âge

moyenne, comparaison

moyenne, intervalle de confiance

multi-états, modèle de survie

multicolinéarité

multicolinéarité parfaite

multidimensional scaling

multinomiale, régression logistique

N

NA

nom, indexation

nombre entier

nombre réel

normale, loi

normalité, test de Shapiro-Wilk

notation formule

notation scientifique

noyau, estimation

nuage de points

numeric

numérique, variable

O

observation

observations répétées, modèle

odds ratio

odds ratio, intervalle de confiance

opérateur de comparaison

opérateur logique

optimal matching

optimal, appariement

ordinaire, régression logistique

ordinale, régression logistique

ordonner le tri à plat

P

package

palette de couleurs

PAM

partition

Partitioning Around Medoids

pas à pas, sélection descendante

patron

perte relative d’inertie

Phi², distance

pirate, graphique

pirateplot

plan d’échantillonnage

plan factoriel

poids de réplication

points, nuage de

pondération

pooled variance

position, indexation

projets

prompt

proportion, intervalle de confiance

proportion, test de comparaison

proxy

Q

qualitative, variable

quantile

quantitative, variable

quartile

R

R Markdown

rapport des cotes

raster

recodage de variables

recyclage

recycling rule

réel, nombre

référence, modalité

régression linéaire

régression logistique

régression logistique binaire

régression logistique multinomiale

régression logistique ordinaire

régression logistique ordinale

régression, droite

régulière, expression

relatif, risque

relation fonctionnelle

répartition empirique, fonction

répertoire de travail

réplication, poids

résidus de Schoenfeld

résidus du modèle

résidus, test du Chi²

résolution

ressemblance

révolu, âge

risque relatif

S

SAS, fichier

saut d’inertie

Schoenfeld, résidus

scientifique, notation

script

scripts

secteur, diagramme

section

sélection descendante pas à pas

séparateur de champs

séparateur décimal

séquence, analyse

séquence, tapis

Shapiro-Wilk, test de normalité

similarité, indice

sous-échantillon

SPSS, fichier

statistique bivariée

statistique descriptive

statistique univariée

strate

stratifié, échantillonnage

structure d’un objet

Student, test t

Student, test-t

survie, analyse

survie, modèle multi-états

T

tableau croisé

tableau croisé, coefficient de contingence de Cramer

tableau croisé, graphique en mosaïque

tableau croisé, test exact de Fisher

tableau de donnée

tableau de données, fusion

tableau de données, tri

tableau de fréquences

tagged missing value

tagged NA

tapis

task view

test d’égalité des variances

test de comparaison de deux proportions

test de normalité de Shapiro-Wilk

test de Wilcoxon/Mann-Whitney

test du Chi²

test du Chi², résidus

test exact de Fisher

test t de Student

texte

texte tabulé, fichier

texte, fichier

tibble

tidy data

tidyverse

total

trajectoire biographique

transversale, entropie

tri à plat

tri à plat, ordonner

U

univariée, statistique

V

valeur booléenne

valeur logique

valeur manquante

valeur manquante déclarée

valeur, étiquette

variable

variable catégorielle

variable d’intérêt

variable explicative

variable labellisée

variable numérique

variable qualitative

variable quantitative

variable, étiquette

variable, recodage

variance

variance inflation factor

variance, analyse de

variance, pooled

variance, test d’égalité

vecteur

vecteur labellisé

vector

viewer

VIF

violin plot

violon, graphique en

visionneusee

W

Ward, méthode

Wilcoxon, test